- Inversion Count for an array indicates how far (or close) the array is from being sorted. If the array is already sorted, then the inversion count is 0.
- But if the array is sorted in the reverse order, the inversion count is the maximum.
- Formally speaking, two elements a[i] and a[j] form an inversion if a[i] > a[j] and i < j
Input: arr[] = {8, 4, 2, 1}
Output: 6
Explanation: Given array has six inversions:
(8, 4), (4, 2), (8, 2), (8, 1), (4, 1), (2, 1).
Input: arr[] = {3, 1, 2}
Output: 2
Explanation: Given array has two inversions:
(3, 1), (3, 2)
- Divide the array into two equal or almost equal halves in each step until the base case is reached.
- Create a function merge that counts the number of inversions when two halves of the array are merged, create two indices i and j.
- i is the index for the first half, and j is an index of the second half.
- If a[i] is greater than a[j], then there are (mid – i) inversions. because left and right subarrays are sorted.
- All the remaining elements in left-subarray (a[i+1], a[i+2] … a[mid]) will be greater than a[j].
- Create a recursive function to divide the array into halves and find the answer by summing the number of inversions is the first half, the number of inversion in the second half and the number of inversions by merging the two.
- The base case of recursion is when there is only one element in the given half.
- Print the answer
- O(n log n), The algorithm used is divide and conquer, So in each level, one full array traversal is needed, and there are log n levels, so the time complexity is O(n log n).
- O(n), Temporary array.
- Recursive program to replace all occurrences of pi with 3.14 in a given string
Input : str = “pippppiiiipi”
Output : 3.14ppp3.14iii3.14
Input : str = “pip”
Output : 3.14p
Input : str = “xpix”
Output : x3.14x
- If the first character is ‘p’ then just put that character in front of the answer which came from recursion.
- Keep the first character of the string with yourself and pass the rest of the string to recursion.
- BASE CASE: - If string of ith position is '\0' and i+1th position is '\0' then return.
- Else the first character is ‘p’ and the first character of the part passed to recursion is ‘i’ then replace “pi” with “3.14”
- O(n).
- O(n).
- Tower of Hanoi is a mathematical game or puzzle involving three sticks and a number of different discs,
which can slip on any stick/rod. The paradox begins with discs embedded in the same object in a declining size(descending order),
the smallest at the top, thus almost showing a conical shape.
Here are three simple rules:
- Only one disk can be moved at a time.
- Each movement involves taking a disk above one of the stacks and placing it on top of another stack.
In other words, the disk can only be moved if it is the highest disk in the stack. - No larger disk can be placed on a smaller disk.
Input : 2
Output : Disk 1 moved from X to Y
Disk 2 moved from X to Z
Disk 1 moved from Y to Z
Explanation:
Taking the example for 2 disks :
Let rod 1 = 'X', rod 2 = 'Y', rod 3 = 'Z'.
Step 1 : Shift first disk from 'X' to 'Y'.
Step 2 : Shift second disk from 'X' to 'Z'.
Step 3 : Shift first disk from 'Y' to 'Z'.
The pattern here is :
Shift 'n-1' disks from 'X' to 'Y'.
Shift last disk (nth) from 'X' to 'Y'.
Shift 'n-1' disks from 'Y' to 'Z'.
START
Procedure Hanoi(disk, source, destination, auxillary)
IF disk == 1, THEN
move disk from source to destination
ELSE
Hanoi(disk - 1, source, auxillary, destination) // Step 1
move disk from source to destination // Step 2
Hanoi(disk - 1, auxillary, destination, source) // Step 3
END IF
END Procedure
STOP
- O(n).
- O(n).
- The Tower of Hanoi puzzle is sensitive to previous damage and malfunction. The level of complexity can be easily increased or decreased with additional discs.
- The Hanoi Tower cannot be used independently to understand and evaluate higher brain functions.
-
Brief explainaion about GCD and LCM : The least common multiple (LCM) of two integers is the smallest positive integer that is a multiple of both. The greatest common divisor (GCD) of two integers is the largest positive integer dividing both. The product of the two numbers is the product of the LCM and the GCD.
-
What is Recursion : The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called as recursive function. Using recursive algorithm, certain problems can be solved quite easily. Examples of such problems are Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, etc.
-
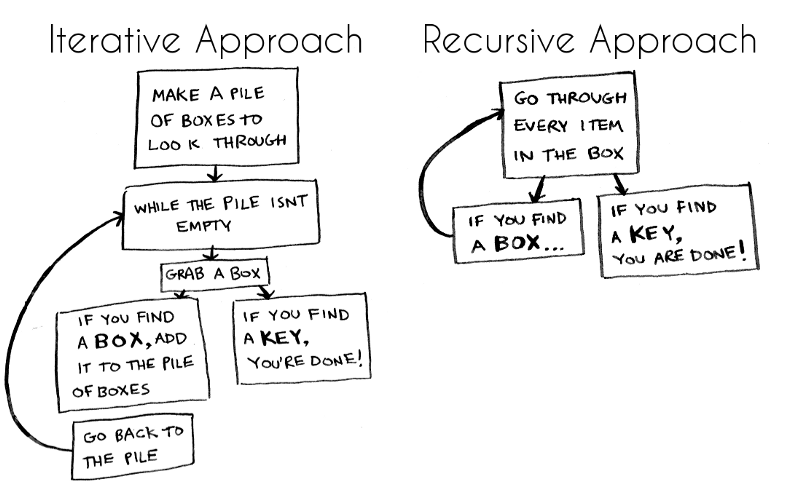
Difference between iterative approach and recursive approach :
- Algorithim for GCD and LCM is given below
- Read two numbers a and b
- If(a is equal to 0) return b
- If(b is equal to 0) return a
- else return (b, a mod b)
- Read two numbrs a and b
- return (a x b) / GCD(a, b)
- O(n).
- O(n).
- The logic used by the program is simple to understand
- time complexity of this program is less compared to other methods for finding GCD and LCM
-The value of the Exponential function can be calculated using Taylor Series.
input-->5,30
output-->144
input-->2,4
output-->6
input-->9,10
output-->19200
- Taylor series is … e^x = 1 + x/1! + x^2/2! + x^3/3! + x^4/4!......
Now consider, the
1st term i.e. 1 - No multiplications here. 2nd term i.e. x/1! - No multiplications here too 3rd term i.e. x^2/2! - Two multiplications here (x*x / 1 * 2) 4th term i.e. x^3/3! - four multiplications here (x * x * x / 1 * 2 * 3) 5th term i.e. x^4/4! - six multiplications here (x * x * x * x / 1 * 2 * 3 * 4) So, if we go till 4th power of x in Taylor series we have to do 2+4+6 = 12 multiplications.
So this number of multiplications will take us O(n^2) time.
But we can reduce the no. of multiplications by using the Horner's rule.
Horner's Rule is just to take common variables and constants outside of the bracket so as to reduce the power the inside the bracket.
We can convert the Taylor series following Horner's Rule to
e^x = 1 + x/1! + x^2/2! + x^3/3! + x^4/4!......
e^x = 1 + x/1 ( 1 + x/2 + x^2/23 + x^3/23*4).........
e^x = 1 + x/1 (1 + x/2 (1 + x/3 + x^2 / 3*4) ).....
e^x = 1 + x/1 (1 + x/2 (1 + x/3 ( 1 + x/4 ) ) ).....
As we can see the total number of multiplications is reduced to just 4 from 12.
So, this will give us O(n) time complexity.
To find this we will determine the total multiplication performed.
e^x = 1 + x/1! + x^2/2! + x^3/3! + …… + until n terms
= 1 + x/1 + x*x/1*2 + x*x*x/1*2*3 + x*x*x*x/1*2*3*4 …… + until n terms
0 0 2 4 8 Number of Multiplications in above terms
So, for n terms total multiplication performed is comparable to sum of n natural numbers (as a parallel series of even numbers is formed).
and we know sum of n natural numbers = n*(n+1)/2 whose order is n2
Hence, the time complexity if this approach is O(n2)
The recursive call will take place n+1 times and hence n + 1 activation records will get created at max. That shows the space complexity is O(n).
- As recursion uses stack, for large numbers, memory may become full due to stack full
- The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,
F(0) = 0, F(1) = 1 F(n) = F(n - 1) + F(n - 2), for n > 1. Given n, calculate F(n).
Example 1 : Input: n = 2
Output: 1
Example 2 : Input: n = 4
Output: 3
- Fibonacci number is a mathematical series in which first two terms are 0 and 1.
- The other terms are obtained by the sum of previous two terms.
- If noticed, we are solving a larger problem by observing the values of smaller problems.
- Hence, Recursion comes into the picture and we solves this problem using this concept.
- O(n).
- O(n), here n is the recursion stack space.
- Given an integer n, return true if it is a power of two. Otherwise, return false. An integer n is a power of two, if there exists an integer x such that n == 2x.
Example 1 : Input: n = 16
Output: true
Example 2 : Input: n = 5
Output: false
- Given a number we have to determine that it can be represented in the power of 2.
- If that number is 1 or 2 obviously, we would be returning true.
- Else we will check the modulo of that number.
- If modulo comes out to be 1, we would return false.
- Another case may be if given no. is 0 we have to return false.
- Call the recursive function for n/2 times.
- O(n).
- O(n), here n is the recursion stack space.
Given an integer n, return true if it is a power of three. Otherwise, return false. An integer n is a power of three, if there exists an integer x such that n == 3x.
Example 1 : Input: n = 13 Output: false
Example 2 : Input: n = 27 Output: true
- Given a number we have to determine that it can be represented in the power of 3.
- If that number is 1 or 3 then obviously, we would be returning true.
- Else we will check the modulo of that number.
- If modulo is not equals to 0 , we would return false.
- Another case may be if given no. is 0 we have to return false.
- Call the recursive function for n/3 times.
- Time Complexity : O(N)
- Space Complexity : O(N) here N is the recursion stack space.
Given an array arr[] of length N and a number K, the task is to find all the subsequences of the array whose sum of elements is K using recursion.
Input: arr[] = {1, 2, 3}, K = 3
Output:
1 2
3
Input: arr[] = {17, 18, 6, 11, 2, 4}, K = 6
Output:
2 4
6
-The idea is to use the jagged array to store the subsequences of the array of different lengths.
-For every element in the array, there are mainly two choices for it that are either to include in the subsequence or not.
-Apply this for every element in the array by reducing the sum, if the element is included otherwise search for the subsequence without including it.
-O(n^2) as this is a recursive solution for the problem. We are using recursion to iterate over all the subsequences and then finding the desired one.
-O(n)