Skip to content

Latest commit

 

History

History
 
 

Binary_Search_Trees

README.md

Binary Search Trees

A Binary Search Tree (BST) is a tree in which all the nodes follow the followig properties −

  • The left sub-tree of a node has a key less than or equal to its parent node's key.
  • The right sub-tree of a node has a key greater than to its parent node's key.

Example: Construct a Binary Search Tree by inserting the following sequence of numbers

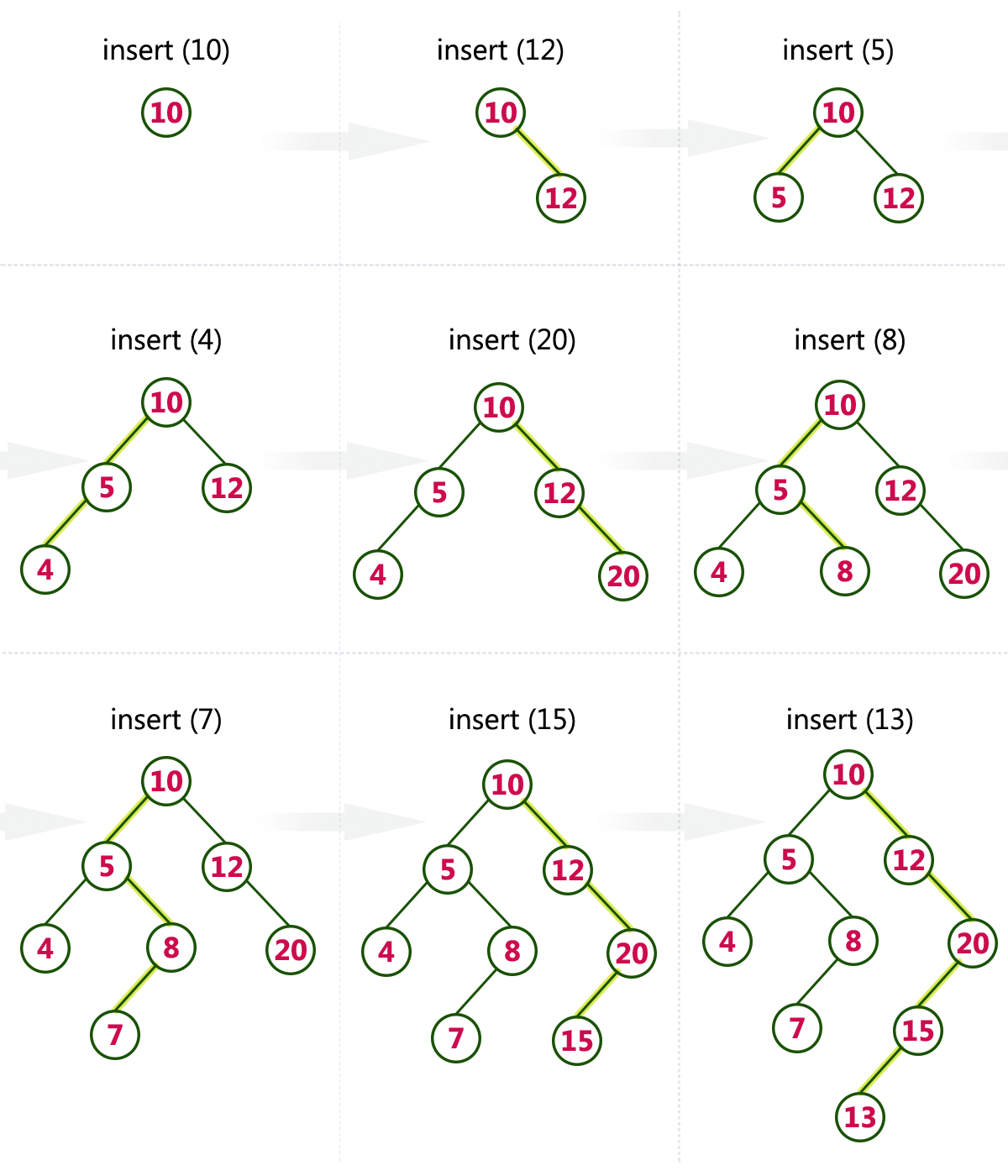
 10,12,5,4,20,8,7,15 and 13

Insertion

Basic Operations

Following are the basic operations of a tree −

1. Search

The search operation is performed as follows

  • Read the search element from the user.
  • Compare the search element with the value of root node in the tree.
  • If both are matched, then display "Given node is found!!!" and terminate the function
  • If both are not matched, then check whether search element is smaller or larger than that node value.
  • If search element is smaller, then continue the search process in left subtree.
  • If search element is larger, then continue the search process in right subtree.
  • Repeat the same until we find the exact element or until the search element is compared with the leaf node
  • If we reach to the node having the value equal to the search value then display "Element is found" and terminate the function.
  • If we reach to the leaf node and if it is also not matched with the search element, then display "Element is not found" and terminate the function.T

2. Insert

The insertion operation is performed as follows

  • Create a newNode with given value and set its left and right to NULL.
  • Check whether tree is Empty.
  • If the tree is Empty, then set root to newNode.
  • If the tree is Not Empty, then check whether the value of newNode is smaller or larger than the node (here it is root node).
  • If newNode is smaller than or equal to the node then move to its left child. If newNode is larger than the node then move to its right child.
  • Repeat the above steps until we reach to the leaf node (i.e., reaches to NULL).
  • After reaching the leaf node, insert the newNode as left child if the newNode is smaller or equal to that leaf node or else insert it as right child.

3. Delete

Case 1: Deleting a Leaf node (A node with no children)

  • Find the node to be deleted using search operation
  • Delete the node using free function (If it is a leaf) and terminate the function.

Case 2: Deleting a node with one child

  • Find the node to be deleted using search operation
  • If it has only one child then create a link between its parent node and child node.
  • Delete the node using free function and terminate the function.

Case 3: Deleting a node with two children

  • Find the node to be deleted using search operation
  • If it has two children, then find the largest node in its left subtree (OR) the smallest node in its right subtree.
  • Swap both deleting node and node which is found in the above step.
  • Then check whether deleting node came to case 1 or case 2 or else goto step 2
  • If it comes to case 1, then delete using case 1 logic.
  • If it comes to case 2, then delete using case 2 logic.
  • Repeat the same process until the node is deleted from the tree.

4. Traversal

There are mainly three types of tree traversals.

1. Pre-order traversal

In this traversal technique the traversal order is root-left-right

- Process data of root node
- First, traverse left subtree completely
- Then, traverse right subtree

void perorder(struct node*root)
{
    if(root)
    {
        printf("%d ",root->data);    //Printf root->data
        preorder(root->left);       //Go to left subtree
        preorder(root->right);     //Go to right subtree
    }
}
2. Post-order traversal

In this traversal technique the traversal order is left-right-root.

  • Process data of left subtree
  • First, traverse right subtree
  • Then, traverse root node
void postorder(struct node*root)
{
    if(root)
    {
        postorder(root->left);      //Go to left sub tree
        postorder(root->right);    //Go to right sub tree
        printf("%d ",root->data); //Printf root->data
    }
}
3. In-order traversal

In in-order traversal, do the following:

  • First process left subtree (before processing root node)
  • Then, process current root node
  • Process right subtree
void inorder(struct node*root)
{
    if(root)
    {
        inorder(root->left);        //Go to left subtree
        printf("%d ",root->data    //Printf root->data
        inorder(root->right);     //Go to right subtree
    }
}

Implementation