We read every piece of feedback, and take your input very seriously.
To see all available qualifiers, see our documentation.
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
王卓老师数据结构课视频讲解
/** * @param {number} numCourses * @param {number[][]} prerequisites * @return {boolean} */ const canFinish = (numCourses, prerequisites) => { const inDegree = new Array(numCourses).fill(0); // 用于存储每个顶点的入度 const map = {} // 用来存储图的连接关系 k:顶点,v:以k为顶点的出度所连接的点 for(let i = 0; i < prerequisites.length; i++){ inDegree[prerequisites[i][0]]++; if(map[prerequisites[i][1]]){ map[prerequisites[i][1]].push(prerequisites[i][0]); // 添加依赖它的后续课 }else{ map[prerequisites[i][1]] = [prerequisites[i][0]]; } } const queue = [] let num = 0; // 选课数量 for(let i = 0; i < inDegree.length; i++){ // 所有入度为0的课入列 if(inDegree[i] == 0){ queue.push(i); } } while(queue.length){ let top = queue.shift(); // 当前选的课,出列 let toDegree = map[top]; // 获取这门课对应的后续课 num++; if(toDegree){ for(let i = 0; i < toDegree.length; i++){ inDegree[toDegree[i]]--; if(inDegree[toDegree[i]] == 0){ queue.push(toDegree[i]); } } } } return num == numCourses; }
视频讲解
/** * @param {number[][]} times * @param {number} n * @param {number} k * @return {number} */ var networkDelayTime = function(times, n, k) { const graph = new Array(n + 1).fill(0).map(m => new Array(n + 1).fill(-1)); const distance = new Array(n + 1).fill(-1); // 存储k到所有节点的距离,下标对应节点,值代表距离 const used = new Array(n + 1).fill(false); // 初始化二维矩阵 for(let i = 0; i < times.length; i++){ graph[times[i][0]][times[i][1]] = times[i][2]; } // k点到其他所有节点的距离 for(let i = 1; i <= n; i++){ distance[i] = graph[k][i]; } distance[k] = 0; // 自己到自己的距离为0 used[k] = true; // k节点已被访问 // 遍历除k之外的n - 1个节点 for(let j = 1; j < n; j++){ let minDistanceNode = 1; // 默认设置为第一个节点 let minDistance = Infinity; // 到最近节点的距离 for(let i = 1; i <= n; i++){ if(!used[i] && distance[i] != -1 && distance[i] < minDistance){ minDistance = distance[i]; minDistanceNode = i; } } used[minDistanceNode] = true; for(let i = 1; i <= n; i++){ if(graph[minDistanceNode][i] != -1){ if(distance[i] != -1){ distance[i] = Math.min(distance[i], distance[minDistanceNode] + graph[minDistanceNode][i]); }else{ // 2->4 = 2->3 + 3->4 distance[i] = distance[minDistanceNode] + graph[minDistanceNode][i]; } } } } let res = -Infinity; for(let i = 1; i <= n; i++){ if(distance[i] == -1) return -1; res = Math.max(res, distance[i]); } return res; };
The text was updated successfully, but these errors were encountered:
No branches or pull requests
拓扑排序
王卓老师数据结构课视频讲解
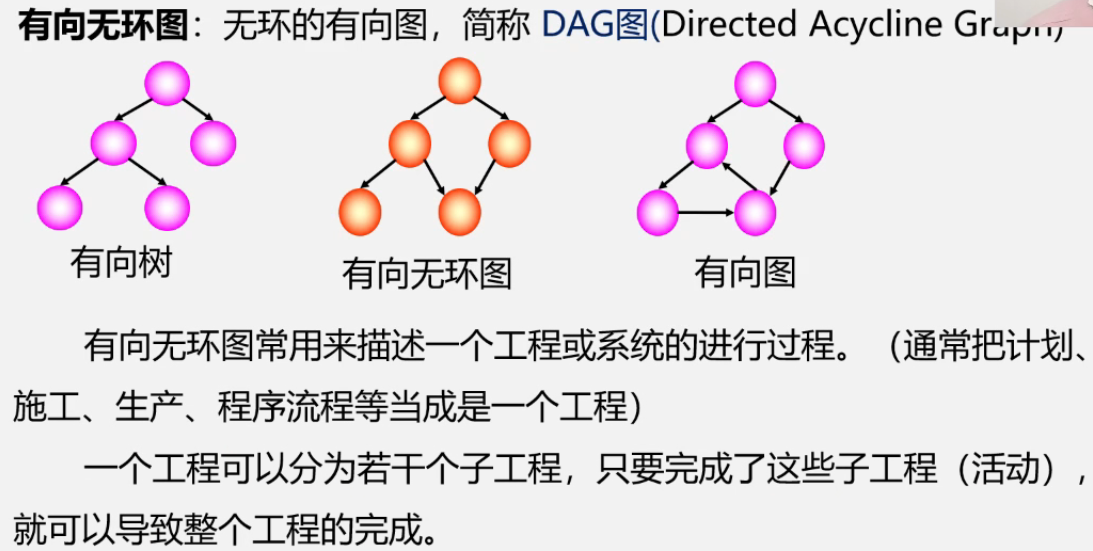

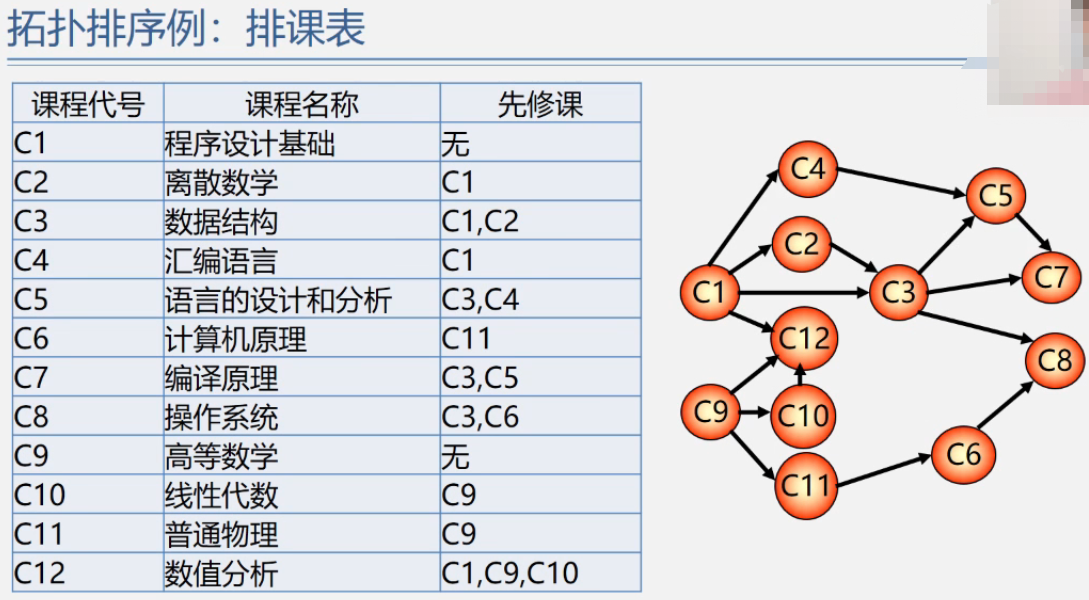

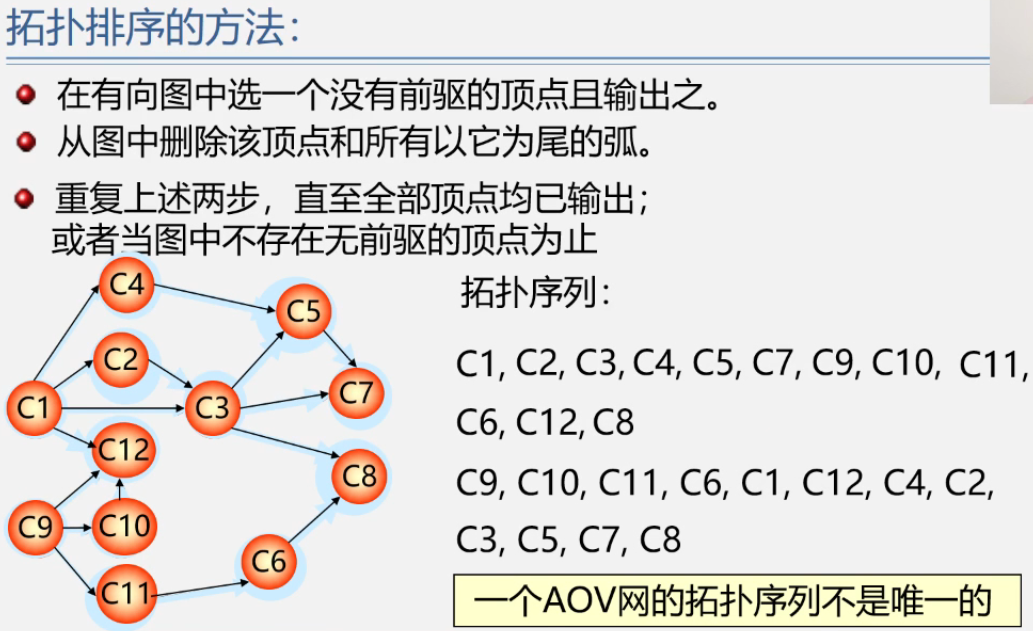

最短路径
视频讲解
关键路径
The text was updated successfully, but these errors were encountered: