sort.md

排序

常考排序

快速排序

import random

def partition(nums, left, right):
    if left >= right:
        return

    pivot_idx = random.randint(left, right)
    pivot = nums[pivot_idx]
    
    nums[right], nums[pivot_idx] = nums[pivot_idx], nums[right]
            
    partition_idx = left
    for i in range(left, right):
        if nums[i] < pivot:
            nums[partition_idx], nums[i] = nums[i], nums[partition_idx]
            partition_idx += 1
            
    nums[right], nums[partition_idx] = nums[partition_idx], nums[right]

    partition(nums, partition_idx + 1, right)
    partition(nums, left, partition_idx - 1)

    return

def quicksort(A):
    partition(A, 0, len(A) - 1)
    return A

if __name__ == '__main__':
    a = [7, 6, 8, 5, 2, 1, 3, 4, 0, 9, 10]
    print(a)
    print(quicksort(a))

归并排序

def merge(A, B):
    C = []
    i, j = 0, 0
    while i < len(A) and j < len(B):
        if A[i] <= B[j]:
            C.append(A[i])
            i += 1
        else:
            C.append(B[j])
            j += 1
    
    if i < len(A):
        C += A[i:]
    
    if j < len(B):
        C += B[j:]
    
    return C

def mergsort(A):
    n = len(A)
    if n < 2:
        return A[:]
    
    left = mergsort(A[:n // 2])
    right = mergsort(A[n // 2:])

    return merge(left, right)

if __name__ == '__main__':
    a = [7, 6, 8, 5, 2, 1, 3, 4, 0, 9, 10]
    print(a)
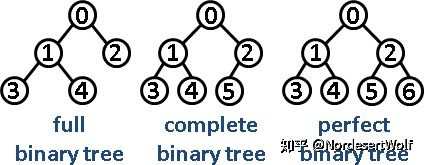
    print(mergsort(a))

堆排序

用数组表示的完美二叉树 complete binary tree

完美二叉树 VS 其他二叉树

动画展示

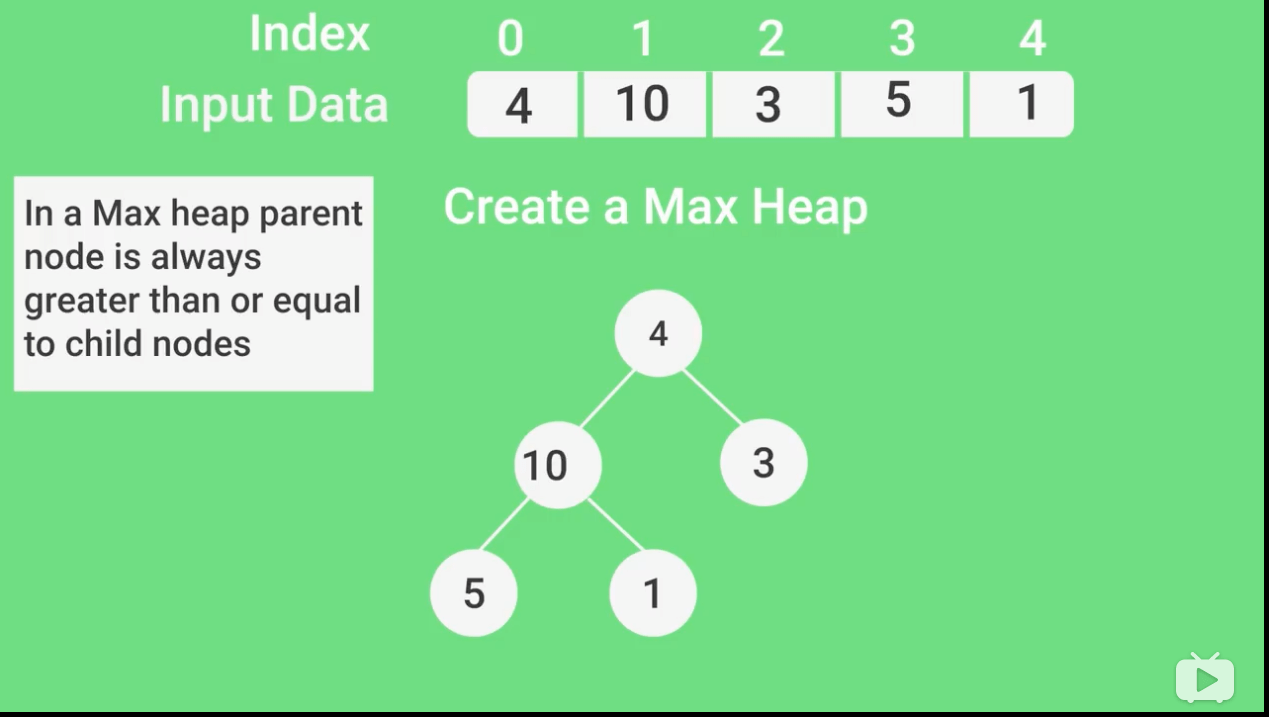
核心代码

def heap_adjust(A, start=0, end=None):
    if end is None:
        end = len(A)
    
    while start is not None and start < end // 2:
        l, r = start * 2 + 1, start * 2 + 2
        swap = None

        if A[l] > A[start]:
            swap = l
        if r < end and A[r] > A[start] and (swap is None or A[r] > A[l]):
            swap = r

        if swap is not None:
            A[start], A[swap] = A[swap], A[start]
            
        start = swap
    
    return

def heapsort(A):

    # construct max heap
    n = len(A)
    for i in range(n // 2 - 1, -1, -1):
        heap_adjust(A, i)
    
    # sort
    for i in range(n - 1, 0, -1):
        A[0], A[i] = A[i], A[0]
        heap_adjust(A, end=i)
    
    return A

# test
if __name__ == '__main__':
    a = [7, 6, 8, 5, 2, 1, 3, 4, 0, 9, 10]
    print(a)
    print(heapsort(a))

题目

kth-largest-element-in-an-array

• 思路 1: sort 后取第 k 个，最简单直接，复杂度 O(N log N) 代码略

• 思路 2: 使用最小堆，复杂度 O(N log k)

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        # note that in practice there is a more efficient python build-in function heapq.nlargest(k, nums)
        min_heap = []
        
        for num in nums:
            if len(min_heap) < k:
                heapq.heappush(min_heap, num)
            else:
                if num > min_heap[0]:
                    heapq.heappushpop(min_heap, num)
        
        return min_heap[0]

• 思路 3: Quick select，方式类似于快排，每次 partition 后检查 pivot 是否为第 k 个元素，如果是则直接返回，如果比 k 大，则继续 partition 小于 pivot 的元素，如果比 k 小则继续 partition 大于 pivot 的元素。相较于快排，quick select 每次只需 partition 一侧，因此平均复杂度为 O(N)。

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        
        k -= 1 # 0-based index
        
        def partition(left, right):
            pivot_idx = random.randint(left, right)
            pivot = nums[pivot_idx]
            
            nums[right], nums[pivot_idx] = nums[pivot_idx], nums[right]
            
            partition_idx = left
            for i in range(left, right):
                if nums[i] > pivot:
                    nums[partition_idx], nums[i] = nums[i], nums[partition_idx]
                    partition_idx += 1
            
            nums[right], nums[partition_idx] = nums[partition_idx], nums[right]
            
            return partition_idx
        
        left, right = 0, len(nums) - 1
        while True:
            partition_idx = partition(left, right)
            if partition_idx == k:
                return nums[k]
            elif partition_idx < k:
                left = partition_idx + 1
            else:
                right = partition_idx - 1

参考

十大经典排序

二叉堆

练习

• 手写快排、归并、堆排序