动态规划:目标和!要求在数列之间加入+ 或者 -,使其和为S。
所有数的总和为sum,假设加法的总和为x,那么可以推出x = (S + sum) / 2。
S 和 sum都是固定的,那此时问题就转化为01背包问题(数列中的数只能使用一次): 给你一些物品(数字),装满背包(就是x)有几种方法。
- 确定dp数组以及下标的含义
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[i]种方法
- 确定递推公式
dp[i] += dp[j - nums[j]]
注意:求装满背包有几种方法类似的题目,递推公式基本都是这样的。
- dp数组如何初始化
dp[0] 初始化为1 ,dp[j]其他下标对应的数值应该初始化为0。
- 确定遍历顺序
01背包问题一维dp的遍历,nums放在外循环,target在内循环,且内循环倒序。
- 举例推导dp数组
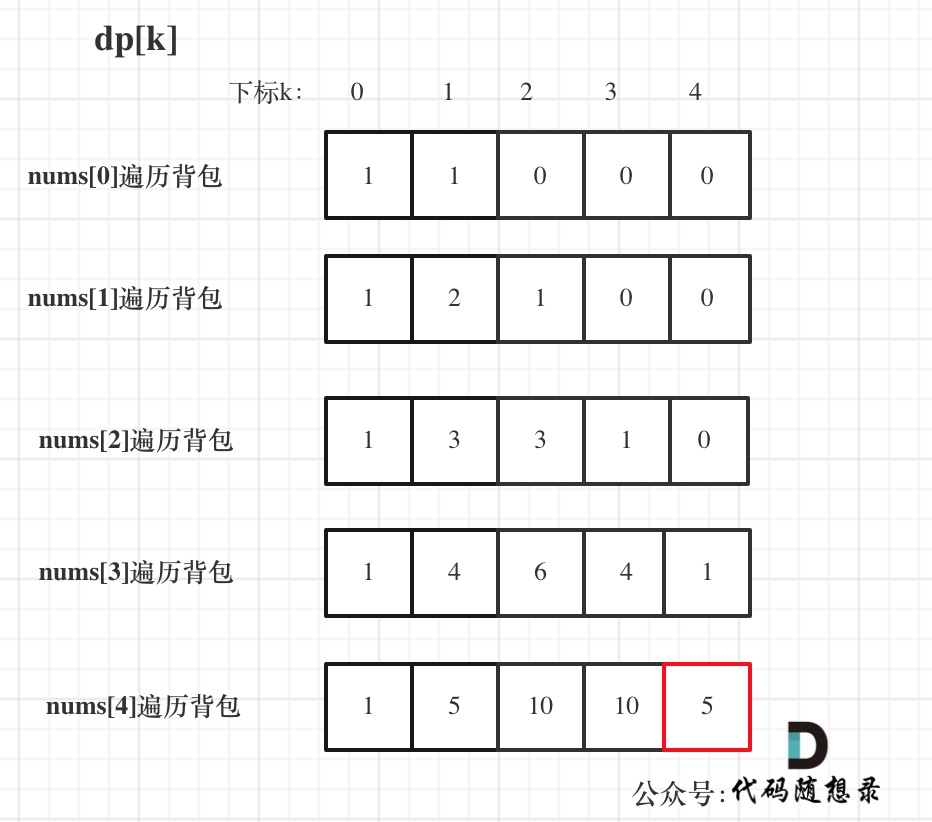
输入:nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:
这道题目动态规划:一和零!算有点难度。
不少同学都以为是多重背包,其实这是一道标准的01背包。
这不过这个背包有两个维度,一个是m 一个是n,而不同长度的字符串就是不同大小的待装物品。
所以这是一个二维01背包!
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
- 确定递推公式
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
字符串集合中的一个字符串0的数量为zeroNum,1的数量为oneNum。
- dp数组如何初始化
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
- 确定遍历顺序
01背包一定是外层for循环遍历物品,内层for循环遍历背包容量且从后向前遍历!
- 举例推导dp数组
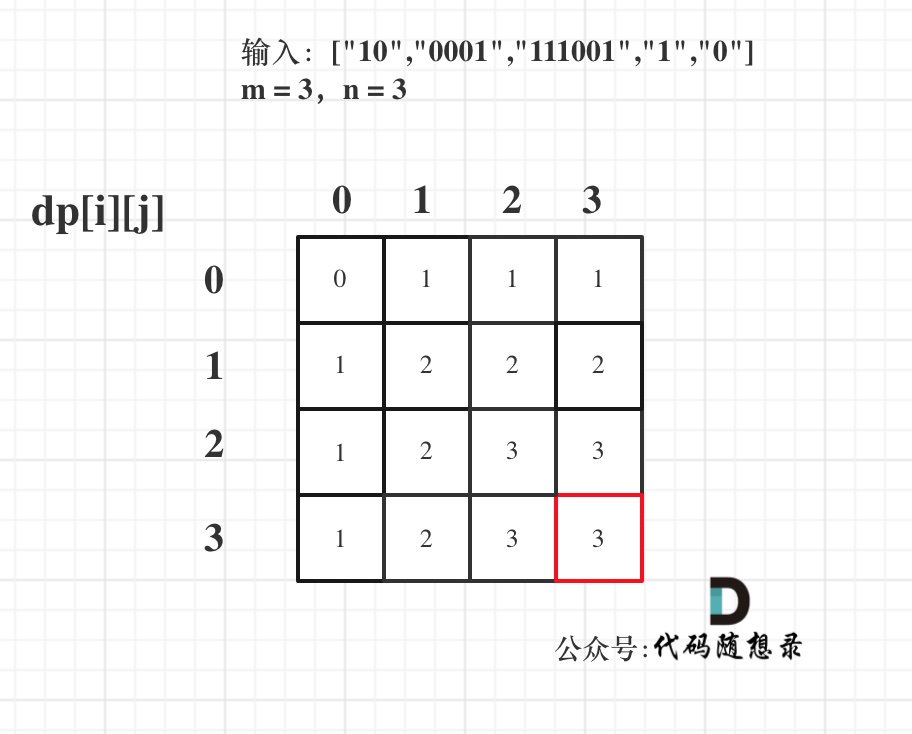
以输入:["10","0001","111001","1","0"],m = 3,n = 3为例
最后dp数组的状态如下所示:
此时01背包我们就讲完了,正式开始完全背包。
在动态规划:关于完全背包,你该了解这些!中我们讲解了完全背包的理论基础。
其实完全背包和01背包区别就是完全背包的物品是无限数量。
递推公式也是一样的,但难点在于遍历顺序上!
完全背包的物品是可以添加多次的,所以遍历背包容量要从小到大去遍历,即:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j < bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}基本网上题的题解介绍到这里就到此为止了。
那么为什么要先遍历物品,在遍历背包呢? (灵魂拷问)
其实对于纯完全背包,先遍历物品,再遍历背包 与 先遍历背包,再遍历物品都是可以的。我在文中动态规划:关于完全背包,你该了解这些!也给出了详细的解释。
这个细节是很多同学忽略掉的点,其实也不算细节了,相信不少同学在写背包的时候,两层for循环的先后循序搞不清楚,靠感觉来的。
所以理解究竟是先遍历啥,后遍历啥非常重要,这也体现出遍历顺序的重要性!
在文中,我也强调了是对纯完全背包,两个for循环先后循序无所谓,那么题目稍有变化,可就有所谓了。
在动态规划:给你一些零钱,你要怎么凑?中就是给你一堆零钱(零钱个数无限),为凑成amount的组合数有几种。
注意这里组合数和排列数的区别!
看到无限零钱个数就知道是完全背包,
但本题不是纯完全背包了(求是否能装满背包),而是求装满背包有几种方法。
这里在遍历顺序上可就有说法了。
- 如果求组合数就是外层for循环遍历物品,内层for遍历背包。
- 如果求排列数就是外层for遍历背包,内层for循环遍历物品。
这里同学们需要理解一波,我在文中也给出了详细的解释,下周我们将介绍求排列数的完全背包题目来加深对这个遍历顺序的理解。
相信通过本周的学习,大家已经初步感受到遍历顺序的重要性!
很多对动规理解不深入的同学都会感觉:动规嘛,就是把递推公式推出来其他都easy了。
其实这是一种错觉,或者说对动规理解的不够深入!
我在动规专题开篇介绍关于动态规划,你该了解这些!中就强调了 递推公式仅仅是 动规五部曲里的一小部分, dp数组的定义、初始化、遍历顺序,哪一点没有搞透的话,即使知道递推公式,遇到稍稍难一点的动规题目立刻会感觉写不出来了。
此时相信大家对动规五部曲也有更深的理解了,同样也验证了Carl之前讲过的:简单题是用来学习方法论的,而遇到难题才体现出方法论的重要性!