无处不在的数字签名

一、为什么需要数字签名？

从上一篇文章里面我们知道，消息认证码可以识别篡改或者发送者身份是否被伪装，也就是验证消息的完整性，还可以对消息进行认证。但是消息认证码的缺陷就在于它的共享密钥上面。由于共享密钥的原因，导致无法防止抵赖。

数字签名就是为了解决抵赖的问题的。解决的方法就是让通信双方的共享密钥不同，从密钥上能区分出谁是谁。

二、什么是数字签名？

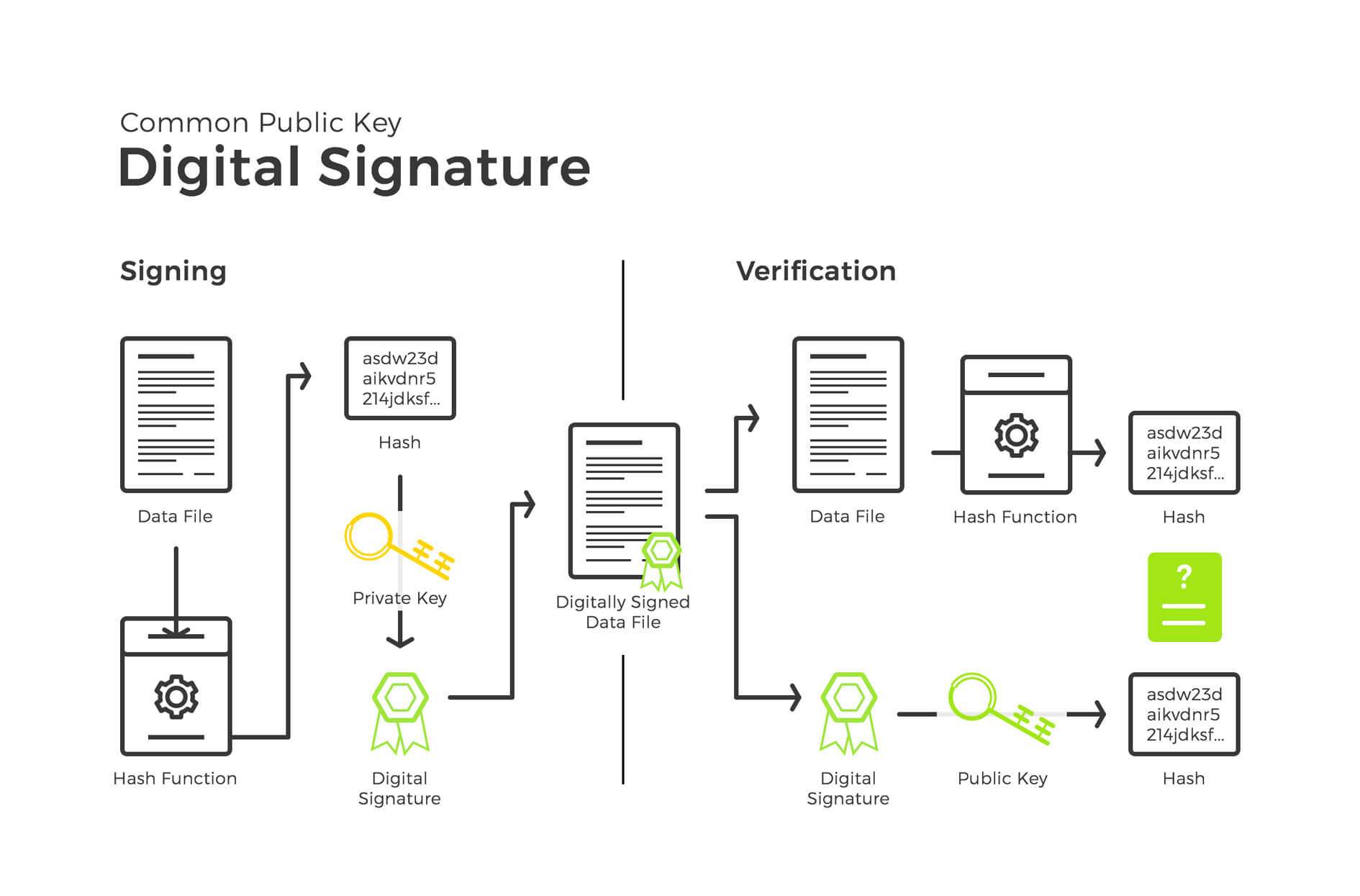
数字签名相当于现实世界中的盖章、签名的功能在计算机世界中进行实现的技术。数字签名可以识别篡改、伪装、防止抵赖。

在数字签名中，有 2 种行为：

生成消息签名的行为
验证消息签名的行为

生成消息签名的人是由消息发送者完成的，也称为“对消息签名”。生成签名就是根据消息内容计算数字签名的值。

验证数字签名的人是第三方。第三方验证消息的来源是否属于发送者。验证结果可以是成功，也可以是失败。

数字签名对签名密钥和验证密钥进行了区分，使用验证密钥是无法生成签名的。签名密钥只能由签名人持有，而验证密钥则是任何需要验证签名的人都可以持有。

	私钥	公钥
公钥密钥	接收者解密时使用	发送者加密时使用
数字签名	签名者生成签名时使用	验证者验证签名时使用
谁持有密钥？	个人持有	只要需要，任何人都可以持有

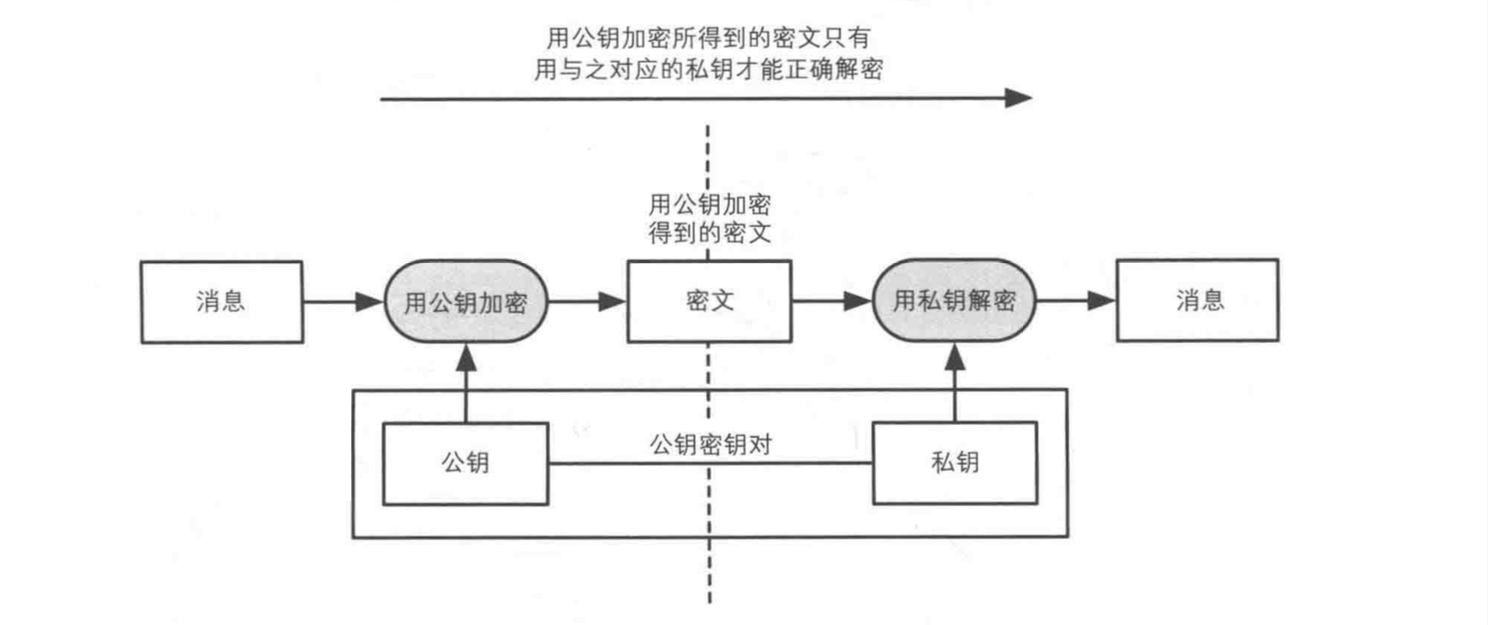
严格的来说，RSA 算法中公钥加密和数字签名正好是完全相反的关系，但是在其他公钥算法中有可能和数字签名不是完全相反的关系。

在公钥算法中，公钥用来加密，私钥用来解密。

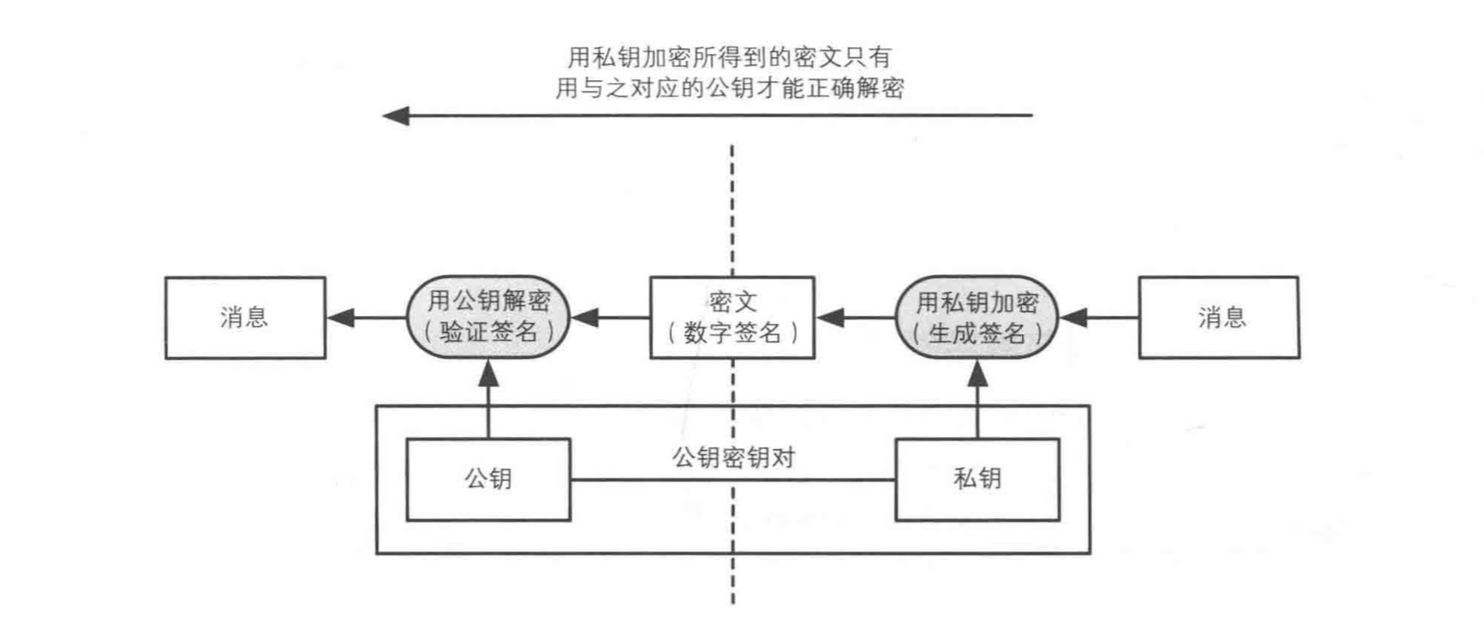
在数字签名中，公钥用来解密(验证签名)，私钥用来加密(生成签名)。

三、生成和验证数字签名

有两种生成和验证数字签名的方法：

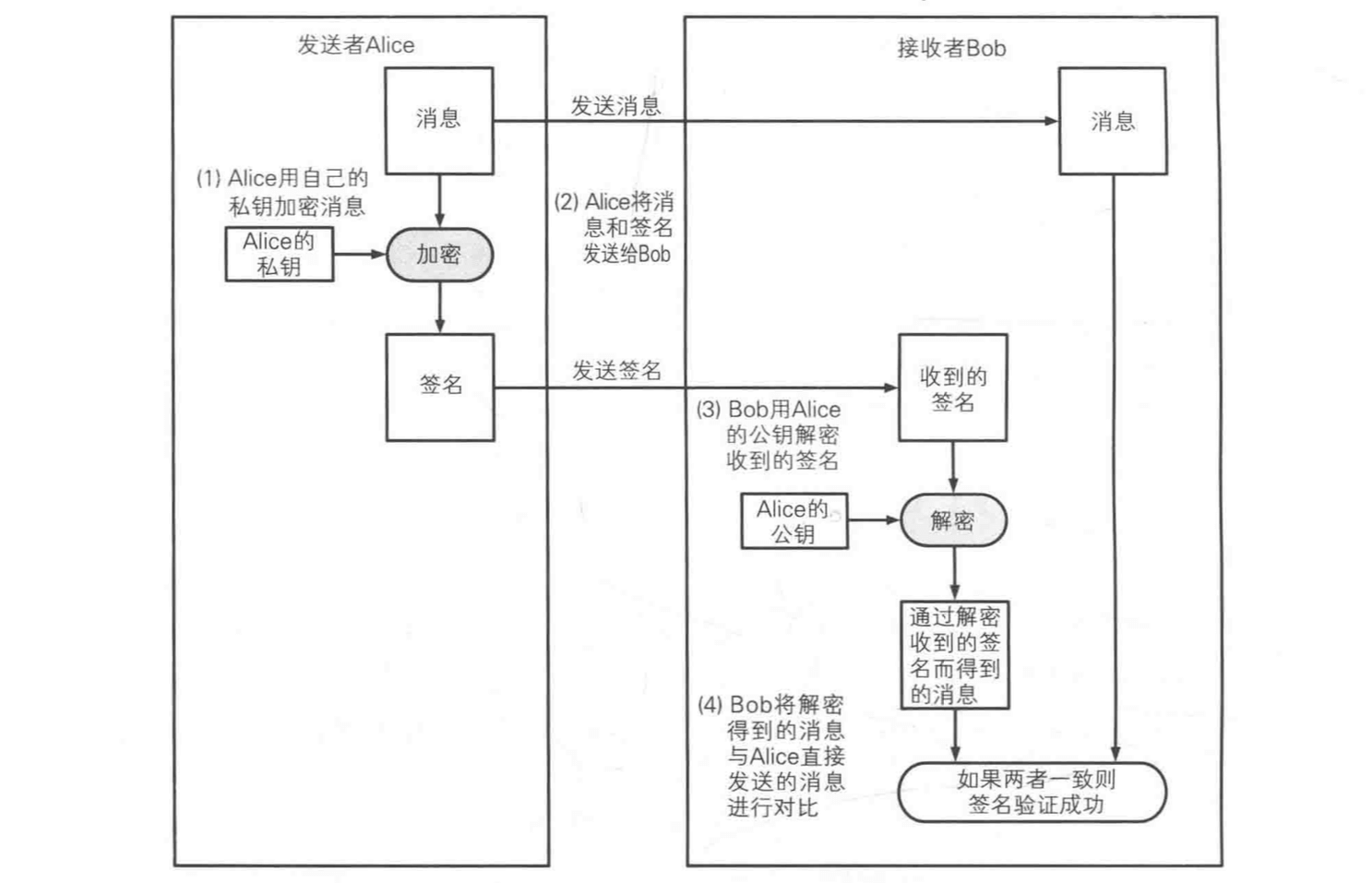
直接对消息签名的方法
对消息的散列值签名的方法

1. 直接对消息签名的方法

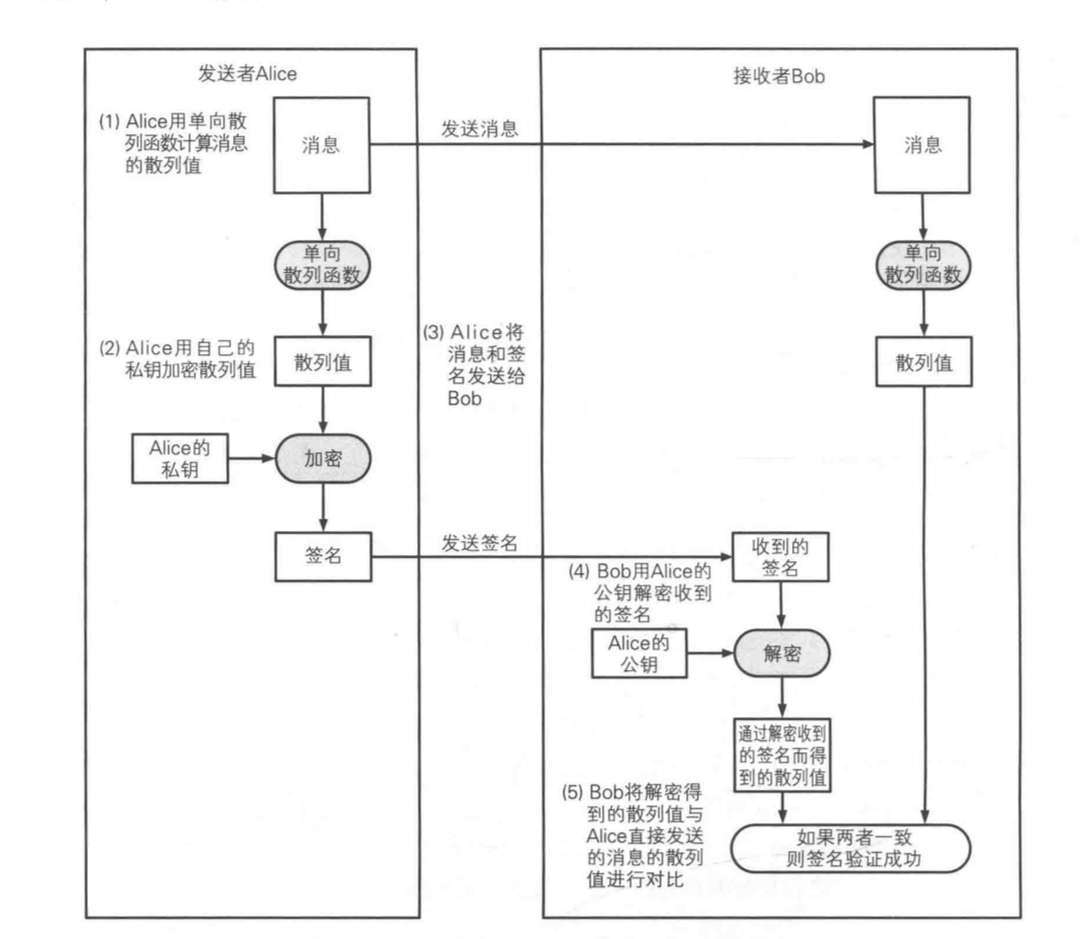
2. 对消息的散列值签名的方法

比较上面 2 种方法，一般都会使用第 2 种方法。原因是因为第 1 种方法要对整个消息进行加密，而且是公钥密钥算法，非常耗时。利用简短的单向散列函数来替代消息本身。再进行加密(对消息进行签名)，会快很多。

对上面的 2 种方法，有一些共性的问题进行解释：

为什么加密以后的密文能够具备签名的意义？
- 数字签名是利用了 “没有私钥的人就无法生成使用该私钥所生成的密文” 这一性质来实现的。生成的密文并非是用于保证机密性，而是用于代表一种只有持有该密钥的人才能生成的信息。所以私钥产生的密文是一种认证符号(authenticator)。
上面方法 2 中消息没有加密就直接发送了，这样不就没法保证消息的机密性了么？
- 数字签名本来就不保证消息的机密性。如果需要保证机密性，可以考虑加密和数字签名结合起来使用。
签名可以随意复制么？
- 数字签名代表的意义是特定的签名者与特定的消息绑定在一起，数字签名虽然可以任意复制，但是它的代表的意义始终不变。
提取出签名，组合任意消息和该签名，这样不就可以伪造签名者的意图了吗？
- 数字签名会识别修改，验证者验证的时候会发现消息和签名的散列值不同，验证失败从而丢弃这条消息。
能否碰撞攻击，同时修改消息和签名，达到骗过验证者的目的？
- 实际上这种方式做不到。首先修改了消息以后，散列值会发生变化。再想拼凑合法的签名，其实是做不到的。因为没有私钥是无法对新的散列值进行加密的。
数字签名签订了以后能反悔么？
- 数字签名本来就是用来防止抵赖的，一旦签署以后，无法抵赖，不能撕毁合同。只能再创建一个声明消息，声明该公钥已经作废的消息并另外加上数字签名。

四、数字签名应用实例

1. 安全信息公告

信息安全组织会在网站上发布一些关于安全漏洞的警告。由于这些信息需要被更多的人知道，所以没有必要对消息进行加密。但是需要防止有人伪装该组织发布虚假信息，这个时候只需要加上数字签名即可。这种对明文消息所施加的签名，一般称为明文签名(clearsign)。

2. 软件下载

为了保证下载软件的安全，不是恶意的病毒，软件作者会对软件加上数字签名。用户在下载完成以后，验证数字签名就能识别出下载的是不是被篡改过的软件。

3. 公钥证书

验证数字签名的时候需要合法的公钥，但是如何才能知道自己拿到的公钥是合法的呢？这个时候就需要把公钥作为信息，对它加上数字签名，得到公钥证书。关于证书的问题再下一篇文章里面详细分析。

4. SSL/TLS

SSL/TLS 在认证服务器身份的时候会使用服务器证书，服务器证书就是加上了数字签名的服务器公钥。

五、数字签名的实现方式

这一章节简单的讲讲用 RSA 公钥算法和单向散列函数生成签名。

1. 用 RSA 生成签名

签名 = 消息^D mod N (用 RSA 生成签名)

上面的 D 和 N 就是签名者的私钥。签名就是对消息的 D 次方求 mod N 的结果。

2. 用 RSA 验证签名

由签名求得的消息 = 签名^E mod N (用 RSA 验证签名)

上面的 E 和 N 就是签名者的公钥。验证者计算签名的 E 次方并求 mod N，得到“由签名求得的消息”。将这个消息和发送者直接发过来的消息进行对比，如果一致就验证成功，不一致就验证失败。

六、其他几种数字签名

1. ElGamal 方式

EIGamal 方式是由 Taher ElGamal 设计的公钥算法，利用了在 mod N 中求离散对数的困难度。ElGamal 方式可以被用于公钥密码和数字签名。

2. DSA

DSA(Digital Signature Algorithm)是一种数字签名的算法。是由 NIST(National Institute of Standards and Technology，美国国家标准技术研究所)于 1991 年制定的数字签名规范(Digital Signature Standard，DSS)。DSA 是 Schnorr 算法和 ElGamal 方式的变体，只能用于数字签名，不能进行加密解密。

和 DH 算法类似，DSA 算法主要了解的也是其参数。通过参数文件生成密钥对。p、q、g 是公共参数，通过参数会生成密钥对，DSA 的公共参数和 DH 的公共参数很像，通过公共参数能够生成无数个密钥对，这是一个很重要的特性。

p 是一个很大的质数，这个值的长度建议大于等于 1024 比特(必须是 64 比特的倍数)，p-1 必须是 q 的倍数，q 的长度必须是 160 比特。而 g 是一个数学表达式的结果，数值来自 p 和 q。

DSA算法中应用了下述参数：

p：L 比特长的素数。L 是 64 的倍数，范围是 512 到 1024；
q：p – 1 的 160 比特的素因子；
g：g = h^((p-1)/q) mod p，h 满足 h < p – 1, h^((p-1)/q) mod p > 1；
x：x < q，x 为私钥；
y：y = g^x mod p ，( p, q, g, y )为公钥；
H( x )：One-Way Hash函数。DSS 中选用 SHA( Secure Hash Algorithm )。

DSA 的密钥对生成就取决于这三个公共参数 p、q、g。计算签名和验证签名也依赖参数文件。

生成 DSA 密钥对

选取一个随机数作为私钥 x ，0 < x < q。
基于私钥生成公钥，g^x mod p

RSA 算法，DH 算法，DSA 算法都是基于离散数学。

签名生成

生成一个随机数 k，1 < k < q。
计算 r = (g^k mod p) mod q。
计算 s = (k^(-1)(H(m)+xr)) mod q，H 是特定的摘要算法。
签名值就是(r，s)，随同原始消息 m 一起发送。

签名验证

假如 r 和 s 大于 q 或者小于 0，则验证直接失败
计算 w = s^(-1) mod q
计算 u1 = H(m).w mod q
计算 u2 = r.w mod q
计算 v = (g^u1 * y^u2 mod p) mod q
如果 v 等于 r，则签名验证成功，否则失败

3. ECDSA

ECDSA(Elliptic Curve Digital Signature Algorithm)是一种利用椭圆曲线密码来实现的数字签名算法。

就像 DH 算法结合 ECC 一样，DSA 算法也能结合 ECC，称为 ECDSA 数字签名算法。相比 DSA 算法，ECDSA 算法安全性更高。

在 ECDSA 中，有三个参数很重要：

ECDSA 算法选择的命名曲线。
G，椭圆曲线的基点
n，相当于 G 基点的打点操作，n * G = 0

生成 ECDSA 密钥对

选择一个随机数作为私钥 d_{a}，1< d_{a} < n -1
基于私钥生成公钥，Q_{a} = d_{a} * G

签名生成

计算摘要值 e = HASH(m)
获取 z = e 最左边的 L_{n} 位字符，L_{n} 是 n 的长度
生成一个随机数 k，1 < k < n - 1
计算 (x,y) = k * G
计算 r = x mod n
计算 s = k_{-1} (z + r * d_{-1}) mod n
签名值(r，s)

验证签名

假如 r 和 s 小于 1 或者大于 n-1，验证直接失败
获取 z = e 最左边的 L_{n} 位字符
计算 w = s^{-1} mod n
计算 u_{1} = zw mod n
计算 u_{2} = rw mod n
计算 (x,y) = u_{1} * G + u_{2} * Q_{a}
如果 r == x_{1} mod n，则签名验证成功，否则失败

4. Rabin 方式

Rabin 方式是由 M.O.Rabin 设计的公钥算法，利用了在 mod N 中求平方根的困难度。Rabin 方式可以被用于公钥密码和数字签名。

七、对数字签名的攻击

1. 中间人攻击公钥

这里的攻击主要是攻击公钥。如何进行公钥之间的认证，还是需要使用公钥证书。

2. 对单向散列函数的攻击

对单向散列函数进行碰撞攻击，生成另外一条不同的消息，使其与签名所绑定的消息具有相同的散列值。

3. 利用数字签名攻击公钥密码

由于 RSA 和数字签名互为逆向操作。于是可以利用这一性质，对 RSA 进行攻击。让发送者对 RSA 密文进行签名(用私钥加密)，就相当于是 RSA 中的解密操作。

防止这种攻击有几种方法：

不要直接对任何消息进行签名，对散列值进行签名比较安全
公钥密码和数字签名使用不同的密钥对
绝对不要对意思不清楚的消息进行签名，就像在看不懂的合同上任意盖章

4. 潜在伪造

即使签名的对象是无任何意义的消息，例如随机比特序列，如果攻击者能够生成合法的数字签名(即攻击者生成的签名能够正常通过校验)，这也算是对这种签名算法的一种潜在威胁。在用 RSA 来解密消息的数字签名算法中，潜在伪造是可能的。只要将随机比特序列 S 用 RSA 的公钥加密生成密文 M，那么，S 就是 M 的合法数字签名，由于攻击者是可以获取公钥的，因此对数字签名的潜在伪造就实现了。

为了防止这种情况，人们改良了 RSA ，开发出了新的签名算法，RSA-PSS(Probabilistic Signature Scheme)。RSA-PSS 并不是对消息本身进行签名，而是对其散列值进行签名，为了提高安全性，在计算散列值的时候还对消息加盐(salt)。

5. 其他攻击

对公钥密码的攻击都可以用于对数字签名的攻击，例如暴力破解私钥，尝试对 RSA 的 N 进行质因数分解等等

八、数字签名无法解决的问题

数字签名所用到的公钥密码中的公钥需要另外认证，防止中间人攻击。认证用于验证签名的公钥必须属于真正的发送者。

似乎陷入了一个死循环。数字签名用来识别消息篡改，伪装以及防止抵赖。但是我们又必须从没有被伪装的发送者得到没有被篡改的公钥才行。

为了验证得到的公钥是否合法，必须使用证书。证书是将公钥当做一条消息，由一个可信的第三方对其签名后所得到的公钥。

关于证书的话题，下一篇文章再继续展开。

九、OpenSSL 中的 RSA 数字签名

和 RSA 公钥加密不一样，RSA 实现的数字签名技术需要涉及到摘要计算，所以需要指定一个 Hash 算法。下面这个例子用 sha256 Hash 算法。

// 生成一个 RSA 密钥对，密钥长度 1024 长度
$ openssl genrsa -out rsaprivatekey.pem 1024

输出

Generating RSA private key, 1024 bit long modulus (2 primes)
......++++++
.............................................++++++
e is 65537 (0x010001)

-----BEGIN RSA PRIVATE KEY-----
MIICXgIBAAKBgQDbaFOaGiDqwRe+nye9lmLy6mnQT33GGjV+vEDtTP/kog3W5jou
LKduc7Qy/iMDXxVyAddaUjRwkuX6mdVOtDzgbBY/nwOSwvTe9jCD89AM7z0il6iG
7m1JgEEq9zYzmRxO/yfkv8OrlZpfZ6/1jzUKVnjXlGdhkipJqBX19M9/kQIDAQAB
AoGBAM2st6oe0jqeNd8InR1ZK3qhif2vdqzNBta+LHMHGl4+F5EbEvEUBQRCTGr8
1t+jM5xC45iUtPnOiu3nZRE5XlIaGbsklPM3chu0/onBdbXsP5aRSZuIobHP01GV
LFqUsFmVOIAKPONRR8Zn5Ji9FQ5bs6meYBmawC23EWcB/cHRAkEA9AwOFZrIN3XG
0YXkoLTm0eGOWg6zRBUxt9ZwCjhciz/riDWnBqIwHxqourN4ss/XwyPJxmvYXMoW
2dl1KmjYBQJBAOYnVRWMraQSdbeSwTo27tGVME3I6RqJHrs0+4EDH/W79bL778fJ
VMRyTjKhZxbzb7xU0bl9it8rbxN+4yjUmx0CQQC31zDw83Vp2e4Yve05Zq0OZASR
MMu4OOMIIqCqAkUsnM04AXq+E4V+mN2ML1B4GvvlQ1tnfqwxUgceuqJ5fRtlAkAN
ouj0pOgo33sgDE7sjxKpUkiRY0UEcHlkqCf6pd+/5IoTN8AmOzSNiyQ89bkw7+1/
4Bqo/do7jMxBAHSfF7G1AkEAsAx6+LSQHRN8iD1Uno9/VJXkoXV5CMicZIO4OXYT
+z95tcREHgHRX4TmtF4Z9fTX5uQsk8oLgHqG9p4Y+RfJXw==
-----END RSA PRIVATE KEY-----

提取公钥

// 从密钥对中分离出公钥
$ openssl rsa -in rsaprivatekey.pem -pubout -out rsapublickey.pem

输出

生成签名文件

// 对 plain.txt 文件使用 sha256 Hash 算法和签名算法生成签名文件 signature.txt 

$ echo "hello" >> plain.txt
$ openssl dgst -sha256 -sign rsaprivatekey.pem -out signature.txt plain.txt

打开 signature.txt 文件，里面存储的就是签名之后的结果。

l^CãîE<9c><9f>>3^M^?&v{7P`<91> <9c>55g^E^@Ç¦ÈYþ _Ïc`=ÓçÖÄ^[^C¢^MgOÕÂ|^^»ÿ%ä:<92><8a>÷<87>f<89>^M.
¢aO<93>ÕÇÝ&xå[áÜ±ã=.À<82>ÙèEz^E(_^@spøZ9×<93>\©É^]ËIo^Z?(^^1*á¶%¯²©^Wñ¶f7iQKäC`

校验签名文件

// 用相同的摘要算法和签名算法校验签名文件，需要对比签名文件和原始文件
$ openssl dgst -sha256 -verify rsapublickey.pem -signature signature.txt plain.txt

输出

Verified OK

如果怀疑上面校验是否是真的，我们可以用另外一个文件来验证一下签名，比如换一个 txt

// 更换一个 txt 文件再次验证签名
$ openssl dgst -sha256 -verify rsapublickey.pem -signature signature.txt signature.txt

输出

Verification Failure

除去用 sha256 Hash 算法以外，还可以指定 RSASSA-PSS 标准

// 生成 RSA 密钥对
$ openssl genrsa -out rsaprivatekey.pem 2048

输出

Generating RSA private key, 2048 bit long modulus (2 primes)
..........................+++
............................+++
e is 65537 (0x010001)

-----BEGIN RSA PRIVATE KEY-----
MIIEpAIBAAKCAQEAuvYWXiZ7esG+Vv/aiOSwoXV1bURTUimwUumQm1N0lOsy0BC4
yxxjhPxz5UNHCUIGFp39Ux6BRRKxAeD+J13AAte6Ge+hU3hS+b1TN55oVpdTX6Er
1GzpnL6bn/ZCGR7Rd4ml9H58+n6SKowDRecBYQkuOgMkInLl36dHCuvG65h3KYdT
Emhkb8IjUQAMGjGcbJpkAnjmP5k6RxY//sx9/o/kyPKiYSIJDRVJBShg+ADfkuyT
qD1jAYl7LSsN4w27KQIV0r606WZbTYcWzM4wPU30XFvTLDzp7frueSF8hprJiOA/
D6TDaCPbEx9QXeUCvsGCXhTUl7sKkNSSA9jW/wIDAQABAoIBAGVoMyuwHcuwqKgR
sJwNxsxcpGu24qavHAdszlWhh5t6kx4N492vMT+hms8glbgsypab7RqXcjBf+gh1
3ATIMeyYzEVjF5Lpsb/p8+g4EInfHIbDKb3XsUKmlEzISoPLlnwK+ivKK8nGu0s+
lEvnB3V1gFBRAdl5jrunxL3kswl3xAOTPUG7HN8SzhKbW2q15iXeIYdsrGDdNmCW
r4ijcW2xuaCAwRIDG9wMsaU+J0kVBoxqrFcN1t73HdhauDCdHqH7oBYYxCliMvmQ
MainlIcF3hfhS8fPbUm52mepIKjUAw+mpzlNnhPz6tuk5T1dUu/hafdIoBZ9yfK1
n6yw14ECgYEA7igQq/di+YE7XdV3jgqKCOlWFx68M14NRdNcYZhjPHw2F4waqur+
K0FDMLVP/lPfoI3BWIvjp3qSiMbplKVPokMAdJ0kkwiw/zSHaz8NYANTET5RQvs1
akhD/oHiktY/NKEWlpofKj09dzeALWzhvIz7q7b6sjXXTJVQL6DouMECgYEAyPgT
6w+yh1Orf8utnCgd2e7YInl+5RhIZqE4DKeJXjFUhxktimv2d7QJXP7KjAcdjel4
KzQ+nIDody59GZtibLRMU1p7tAHOFKpV7k7D3ZiDqzn9BsRs+GemKAjoY5BroL9b
+Cdc05ksRRSyd37A1C6sbLepbKyzvUmbzTUfv78CgYAqvRPo2HdxkSiHOVTAL9H/
sWgatBBQI5O8MScF+KPuadgHN8RdYdiFCKw3JIKbgI/EL0xASLJtDskXNKMcYuI8
m0uModq7bDbfRZz7uQ/8Z/xTPty0aYJ3dUqGdOalNT+YgUQdeMEZAm5yY4pkHIMS
JDbR5P9uVc0yWCVQts6swQKBgQC1QfKNDtJhddh3YdfKwO/zkJVFurj1nconLn9k
AnNGDk4Dr3TApRFd83aCdpduZjiEty8YIH3cH/QLElXok5nZG2C/yRtLRll9kAgC
8O19XsJa2+lXgjAadzmIYEhhDG/WQuGLVs1FV6BzCfDRD/SRKyt+vsPDbZyLO+mW
0rQ49wKBgQDhWlAtmZKN12tfvHWpnbhj4rfBaSFpYRh4AimgQJyPvjzy/9Edw7i5
YAJosFtocanOpnKbYaZCng5wFra9e9+vwd66Ab80o/ZzAtuNtyxh1+LP2c+XCl8W
dgF4cl4wkopwQ6f8dauG7dKGsP4NunUoXjJO/Ky+PcFgzrAeJ3Z8xA==
-----END RSA PRIVATE KEY-----

分离出公钥

$ openssl rsa -in rsaprivatekey.pem -pubout -out rsapublickey.pem

输出

指定 RSASSA-PSS 标准

// 指定 RSASSA-PSS 标准
$ openssl dgst -sha256 -sign rsaprivatekey.pem -sigopt rsa_padding_mode:pss -out signature.txt plain.txt

打开 signature.txt 文件，里面存储的就是签名之后的结果。

¡°<8f>^W-ý0]ê^Qnà<90><97>N<9e>8^T²»<97>¢<8d>¤¯*S<98>ò.C·=^BñM¸bõ^[<99>Øãp×V²Ð8vz#^Z}¹ÔO¨õò¬<85>^D<8c>¦C^W^K²$^P&BCô$Z4<8b>¢w<9c><91>þz@×<82>ùáÇ¶µ&8<97>Í<8a><95>4ºû7É¿#^X<95>SÜ_s<98>g<9a>lï<91><92>gý^Bm^Yw'1LJ7¹m3+<81>m©¥ë\<96>¼BÄØ<8d>vO»Ü<82><98>¨^K]7ØÖöP¿^F^_[Ñã÷Þ3^^}-´ý<84><9f>^E^[ÖA>^NF<8f>É!<8c>¿ÿÆ,º«õtãäV8ÿ<91><8b>Ã_Å<9f>ï<88>Q^õ<99>^Uê<9c><91>^E)Õ$H¶"ç:hDôU*_FÙ<8a>^LÝU<8f>^H©9%uè^_^C¨V<8d>+yB¨^ZR

验证签名

// 验证签名
$ openssl dgst -sha256 -verify rsapublickey.pem -sigopt rsa_padding_mode:pss -signature signature.txt plain.txt

输出

Verified OK

如果怀疑上面校验是否是真的，我们可以用另外一个文件来验证一下签名，比如换一个 txt，或者不用 PSS 模式去校验，以上两种方法都会校验失败。

// 更换一个 txt 文件再次验证签名
$ openssl dgst -sha256 -verify rsapublickey.pem -sigopt rsa_padding_mode:pss -signature signature.txt signature.txt

// 不用 PSS 模式验证签名
$ openssl dgst -sha256 -verify rsapublickey.pem -signature signature.txt plain.txt

上面两种方式都会校验失败。

十、OpenSSL 中的 DSA 数字签名

使用 OpenSSL 命令了解 DSA 算法。

// 生成参数文件，类似于 DH 参数文件
$ openssl dsaparam -out dsaparam.pem 1024

输出

Generating DSA parameters, 1024 bit long prime
This could take some time
..........+..+.............................+++++++++++++++++++++++++++++++++++++++++++++++++++*
..+..+....+....+.+....+..............+.....+...+.+...................+.+...........+.+..+...+++++++++++++++++++++++++++++++++++++++++++++++++++*

-----BEGIN DSA PARAMETERS-----
MIIBHgKBgQDbXt+UNxsM2KJGR5q76uqWDgmZKSV3vordjqdwirG/ukuRkBrg0p7y
Whhd8s+As+Q0erzE9mQfyKrqnQjAAxBOT/9rjH4hvYcgg0H/uSzWrkRIgZx7/8dF
dnOEH+ORwgQlbxZ+p1k/Le4rJh/dTARRbAjCa+YkAU9ZL8cGnsQvWQIVAJ8v+YVH
YjCApNnLjEBVRTF4kvSpAoGAearp5Wi8BtC77al/P+W/KfxTrp3TmMFwImWG+Fqd
GVa4poqhYEcFGSaZsrnFZGOwT0PgFLvFCzkz0sfn0OeT7haSIwr8lVcnXL3dexWY
ejEeWDa1nCERqAL9r/eO5QldwSgw6muCjNA/A7eghz1E5KQxjYkRQGLdYx+fbC1N
ge4=
-----END DSA PARAMETERS-----

生成密钥对

// 通过参数文件生成密钥对 dsaprivatekey.pem
$ openssl gendsa -out dsaprivatekey.pem dsaparam.pem

输出

Generating DSA key, 1024 bits

-----BEGIN DSA PRIVATE KEY-----
MIIBuwIBAAKBgQDbXt+UNxsM2KJGR5q76uqWDgmZKSV3vordjqdwirG/ukuRkBrg
0p7yWhhd8s+As+Q0erzE9mQfyKrqnQjAAxBOT/9rjH4hvYcgg0H/uSzWrkRIgZx7
/8dFdnOEH+ORwgQlbxZ+p1k/Le4rJh/dTARRbAjCa+YkAU9ZL8cGnsQvWQIVAJ8v
+YVHYjCApNnLjEBVRTF4kvSpAoGAearp5Wi8BtC77al/P+W/KfxTrp3TmMFwImWG
+FqdGVa4poqhYEcFGSaZsrnFZGOwT0PgFLvFCzkz0sfn0OeT7haSIwr8lVcnXL3d
exWYejEeWDa1nCERqAL9r/eO5QldwSgw6muCjNA/A7eghz1E5KQxjYkRQGLdYx+f
bC1Nge4CgYB6o8lSB4HkznXMyVkByLeRo5IE+IQqKcFtM4kD6d4ZukcI2IUHp7bI
jYSjJNyalYTwPcCMgpWJEseC6Xcf90gR39Sz/P2+pWiyCzhJ1CXHlQzwpOIAKuOq
ojwlykrYBZuPuD0Bpo2kUJKyua/Te1b8cfElVMyr7OrCN0HIBIHovQIVAJbryCYW
7s9I2PGsiuz758FMjZ9Z
-----END DSA PRIVATE KEY-----

对私钥文件进行加密

// 对私钥对文件使用 des3 算法进行加密
$ openssl gendsa -out dsaprivatekey2.pem -des3 dsaparam.pem

输出

Generating DSA key, 1024 bits
Enter PEM pass phrase:
Verifying - Enter PEM pass phrase:

----BEGIN DSA PRIVATE KEY-----
Proc-Type: 4,ENCRYPTED
DEK-Info: DES-EDE3-CBC,E06226CA00C80472

xTbh4VYy44X/0sZMmUfuPua9VtunXtcdJ3soFHvjpjBaCgn64/nVbGQYBV1t6TY0
Poic5LmZ+ooVCAxC9EkUid+TzZ3qCWwI3Pdagj8YoNWrak6ayj6j00EZ2HQNs3eI
j2lyIpyetpJCziGvohveEnmFEU6k7DSKdgpJtZv2yayK4L19r8AIcGlgO/o125qH
VP4vJvoEAuFMrxXJP3NgJ0ZcF9fffAZz6sV+lHGVb6B8rWptWwP9QRNGNfdqa5T9
RJAbZrYpvyBlewljDXscB34eYo6PrlItlTWImvJ+KrVA8QLpYditIcjjdlNDYvRq
eC7sgyDGaKNBSk+DDQ5ZKQaI9MEPi34kAqp+esv083WbnXhCkkSzcu5sacxPJJQN
XK0nxP3YSWY7w0L/cDzxnsaT0gl+l3AFvUxDge97iq3hmDGt6BSqLzAQAcn4VDnx
Hc0OQKm3hZalej6iLNenf84SWxC7dc0cRgfReMOXhjik+PsN4eturhDkGzapiHW2
YLVG15f+/XEknnvW5RQ8ttTPB47O7UFxxt4JLw4KE3nsDkGYFweEOwffVWFo3MH8
+uYhp/Inu8Z0bTVUCm5bSA==
-----END DSA PRIVATE KEY-----

提取公钥

// 通过密钥对文件拆分出公钥
$ openssl dsa -in dsaprivatekey.pem -pubout -out dsapublickey.pem

输出

read DSA key
writing DSA key

-----BEGIN PUBLIC KEY-----
MIIBtjCCASsGByqGSM44BAEwggEeAoGBANte35Q3GwzYokZHmrvq6pYOCZkpJXe+
it2Op3CKsb+6S5GQGuDSnvJaGF3yz4Cz5DR6vMT2ZB/IquqdCMADEE5P/2uMfiG9
hyCDQf+5LNauREiBnHv/x0V2c4Qf45HCBCVvFn6nWT8t7ismH91MBFFsCMJr5iQB
T1kvxwaexC9ZAhUAny/5hUdiMICk2cuMQFVFMXiS9KkCgYB5qunlaLwG0LvtqX8/
5b8p/FOundOYwXAiZYb4Wp0ZVrimiqFgRwUZJpmyucVkY7BPQ+AUu8ULOTPSx+fQ
55PuFpIjCvyVVydcvd17FZh6MR5YNrWcIRGoAv2v947lCV3BKDDqa4KM0D8Dt6CH
PUTkpDGNiRFAYt1jH59sLU2B7gOBhAACgYB6o8lSB4HkznXMyVkByLeRo5IE+IQq
KcFtM4kD6d4ZukcI2IUHp7bIjYSjJNyalYTwPcCMgpWJEseC6Xcf90gR39Sz/P2+
pWiyCzhJ1CXHlQzwpOIAKuOqojwlykrYBZuPuD0Bpo2kUJKyua/Te1b8cfElVMyr
7OrCN0HIBIHovQ==
-----END PUBLIC KEY-----

查看私钥文件的信息

// 查看三个公共参数、公钥、私钥
$ openssl dsa -in dsaprivatekey.pem -text

输出

read DSA key
Private-Key: (1024 bit)
priv:
    00:96:eb:c8:26:16:ee:cf:48:d8:f1:ac:8a:ec:fb:
    e7:c1:4c:8d:9f:59
pub:
    7a:a3:c9:52:07:81:e4:ce:75:cc:c9:59:01:c8:b7:
    91:a3:92:04:f8:84:2a:29:c1:6d:33:89:03:e9:de:
    19:ba:47:08:d8:85:07:a7:b6:c8:8d:84:a3:24:dc:
    9a:95:84:f0:3d:c0:8c:82:95:89:12:c7:82:e9:77:
    1f:f7:48:11:df:d4:b3:fc:fd:be:a5:68:b2:0b:38:
    49:d4:25:c7:95:0c:f0:a4:e2:00:2a:e3:aa:a2:3c:
    25:ca:4a:d8:05:9b:8f:b8:3d:01:a6:8d:a4:50:92:
    b2:b9:af:d3:7b:56:fc:71:f1:25:54:cc:ab:ec:ea:
    c2:37:41:c8:04:81:e8:bd
P:
    00:db:5e:df:94:37:1b:0c:d8:a2:46:47:9a:bb:ea:
    ea:96:0e:09:99:29:25:77:be:8a:dd:8e:a7:70:8a:
    b1:bf:ba:4b:91:90:1a:e0:d2:9e:f2:5a:18:5d:f2:
    cf:80:b3:e4:34:7a:bc:c4:f6:64:1f:c8:aa:ea:9d:
    08:c0:03:10:4e:4f:ff:6b:8c:7e:21:bd:87:20:83:
    41:ff:b9:2c:d6:ae:44:48:81:9c:7b:ff:c7:45:76:
    73:84:1f:e3:91:c2:04:25:6f:16:7e:a7:59:3f:2d:
    ee:2b:26:1f:dd:4c:04:51:6c:08:c2:6b:e6:24:01:
    4f:59:2f:c7:06:9e:c4:2f:59
Q:
    00:9f:2f:f9:85:47:62:30:80:a4:d9:cb:8c:40:55:
    45:31:78:92:f4:a9
G:
    79:aa:e9:e5:68:bc:06:d0:bb:ed:a9:7f:3f:e5:bf:
    29:fc:53:ae:9d:d3:98:c1:70:22:65:86:f8:5a:9d:
    19:56:b8:a6:8a:a1:60:47:05:19:26:99:b2:b9:c5:
    64:63:b0:4f:43:e0:14:bb:c5:0b:39:33:d2:c7:e7:
    d0:e7:93:ee:16:92:23:0a:fc:95:57:27:5c:bd:dd:
    7b:15:98:7a:31:1e:58:36:b5:9c:21:11:a8:02:fd:
    af:f7:8e:e5:09:5d:c1:28:30:ea:6b:82:8c:d0:3f:
    03:b7:a0:87:3d:44:e4:a4:31:8d:89:11:40:62:dd:
    63:1f:9f:6c:2d:4d:81:ee
writing DSA key
-----BEGIN DSA PRIVATE KEY-----
MIIBuwIBAAKBgQDbXt+UNxsM2KJGR5q76uqWDgmZKSV3vordjqdwirG/ukuRkBrg
0p7yWhhd8s+As+Q0erzE9mQfyKrqnQjAAxBOT/9rjH4hvYcgg0H/uSzWrkRIgZx7
/8dFdnOEH+ORwgQlbxZ+p1k/Le4rJh/dTARRbAjCa+YkAU9ZL8cGnsQvWQIVAJ8v
+YVHYjCApNnLjEBVRTF4kvSpAoGAearp5Wi8BtC77al/P+W/KfxTrp3TmMFwImWG
+FqdGVa4poqhYEcFGSaZsrnFZGOwT0PgFLvFCzkz0sfn0OeT7haSIwr8lVcnXL3d
exWYejEeWDa1nCERqAL9r/eO5QldwSgw6muCjNA/A7eghz1E5KQxjYkRQGLdYx+f
bC1Nge4CgYB6o8lSB4HkznXMyVkByLeRo5IE+IQqKcFtM4kD6d4ZukcI2IUHp7bI
jYSjJNyalYTwPcCMgpWJEseC6Xcf90gR39Sz/P2+pWiyCzhJ1CXHlQzwpOIAKuOq
ojwlykrYBZuPuD0Bpo2kUJKyua/Te1b8cfElVMyr7OrCN0HIBIHovQIVAJbryCYW
7s9I2PGsiuz758FMjZ9Z
-----END DSA PRIVATE KEY-----

priv 和 pub 相当于密钥对中的私钥和公钥，P、Q、G 都是参数文件中的三个关键参数，这是 DSA 算法的关键。

既然可以查看私钥文件的信息，同理可以查看公钥文件的信息。

// 查看公钥和文件的信息
$ openssl dsa -pubin -in dsapublickey.pem -text

输出

read DSA key
pub:
    7a:a3:c9:52:07:81:e4:ce:75:cc:c9:59:01:c8:b7:
    91:a3:92:04:f8:84:2a:29:c1:6d:33:89:03:e9:de:
    19:ba:47:08:d8:85:07:a7:b6:c8:8d:84:a3:24:dc:
    9a:95:84:f0:3d:c0:8c:82:95:89:12:c7:82:e9:77:
    1f:f7:48:11:df:d4:b3:fc:fd:be:a5:68:b2:0b:38:
    49:d4:25:c7:95:0c:f0:a4:e2:00:2a:e3:aa:a2:3c:
    25:ca:4a:d8:05:9b:8f:b8:3d:01:a6:8d:a4:50:92:
    b2:b9:af:d3:7b:56:fc:71:f1:25:54:cc:ab:ec:ea:
    c2:37:41:c8:04:81:e8:bd
P:
    00:db:5e:df:94:37:1b:0c:d8:a2:46:47:9a:bb:ea:
    ea:96:0e:09:99:29:25:77:be:8a:dd:8e:a7:70:8a:
    b1:bf:ba:4b:91:90:1a:e0:d2:9e:f2:5a:18:5d:f2:
    cf:80:b3:e4:34:7a:bc:c4:f6:64:1f:c8:aa:ea:9d:
    08:c0:03:10:4e:4f:ff:6b:8c:7e:21:bd:87:20:83:
    41:ff:b9:2c:d6:ae:44:48:81:9c:7b:ff:c7:45:76:
    73:84:1f:e3:91:c2:04:25:6f:16:7e:a7:59:3f:2d:
    ee:2b:26:1f:dd:4c:04:51:6c:08:c2:6b:e6:24:01:
    4f:59:2f:c7:06:9e:c4:2f:59
Q:
    00:9f:2f:f9:85:47:62:30:80:a4:d9:cb:8c:40:55:
    45:31:78:92:f4:a9
G:
    79:aa:e9:e5:68:bc:06:d0:bb:ed:a9:7f:3f:e5:bf:
    29:fc:53:ae:9d:d3:98:c1:70:22:65:86:f8:5a:9d:
    19:56:b8:a6:8a:a1:60:47:05:19:26:99:b2:b9:c5:
    64:63:b0:4f:43:e0:14:bb:c5:0b:39:33:d2:c7:e7:
    d0:e7:93:ee:16:92:23:0a:fc:95:57:27:5c:bd:dd:
    7b:15:98:7a:31:1e:58:36:b5:9c:21:11:a8:02:fd:
    af:f7:8e:e5:09:5d:c1:28:30:ea:6b:82:8c:d0:3f:
    03:b7:a0:87:3d:44:e4:a4:31:8d:89:11:40:62:dd:
    63:1f:9f:6c:2d:4d:81:ee
writing DSA key
-----BEGIN PUBLIC KEY-----
MIIBtjCCASsGByqGSM44BAEwggEeAoGBANte35Q3GwzYokZHmrvq6pYOCZkpJXe+
it2Op3CKsb+6S5GQGuDSnvJaGF3yz4Cz5DR6vMT2ZB/IquqdCMADEE5P/2uMfiG9
hyCDQf+5LNauREiBnHv/x0V2c4Qf45HCBCVvFn6nWT8t7ismH91MBFFsCMJr5iQB
T1kvxwaexC9ZAhUAny/5hUdiMICk2cuMQFVFMXiS9KkCgYB5qunlaLwG0LvtqX8/
5b8p/FOundOYwXAiZYb4Wp0ZVrimiqFgRwUZJpmyucVkY7BPQ+AUu8ULOTPSx+fQ
55PuFpIjCvyVVydcvd17FZh6MR5YNrWcIRGoAv2v947lCV3BKDDqa4KM0D8Dt6CH
PUTkpDGNiRFAYt1jH59sLU2B7gOBhAACgYB6o8lSB4HkznXMyVkByLeRo5IE+IQq
KcFtM4kD6d4ZukcI2IUHp7bIjYSjJNyalYTwPcCMgpWJEseC6Xcf90gR39Sz/P2+
pWiyCzhJ1CXHlQzwpOIAKuOqojwlykrYBZuPuD0Bpo2kUJKyua/Te1b8cfElVMyr
7OrCN0HIBIHovQ==
-----END PUBLIC KEY-----

输出的内容中，pub、P、Q、G 四个参数和私钥输出的内容是一致的。

最后验证 DSA 签名算法。这里和 RSA 是差不多的

// DSA 进行签名
$ openssl dgst -sha256 -sign dsaprivatekey.pem -out signature.txt plain.txt

输出

0-^B^T^QÉ:wÇ^K^F^AÆ<88>Ê^C!0Hø>,$^W^B^U^@<8d>Ùy
^@H^W^W^Dàø'mqî_}^Y¹m

校验签名

// 验证签名
$ openssl dgst -sha256 -verify dsapublickey.pem -signature signature.txt plain.txt

输出

Verified OK

如果怀疑上面校验是否是真的，我们可以用另外一个文件来验证一下签名，比如换一个 txt

// 更换一个 txt 文件再次验证签名
$ openssl dgst -sha256 -verify dsapublickey.pem -signature signature.txt signature.txt

输出

Verification Failure

十、OpenSSL 中的 ECDSA 数字签名

生成 ECDSA 私钥

// 直接生成 ECDSA 私钥，不用预先生成 ECC 参数文件
$ openssl ecparam -name secp256k1 -genkey -out ecdsa_priv.pem

输出

// secp256k1.pem
-----BEGIN EC PARAMETERS-----
BgUrgQQACg==
-----END EC PARAMETERS-----

// ecdsa_priv.pem
-----BEGIN EC PARAMETERS-----
BgUrgQQACg==
-----END EC PARAMETERS-----
-----BEGIN EC PRIVATE KEY-----
MHQCAQEEIAU0ftIIbLdCROYOZcGcc+4JjAsTvYI1pH9Ejbx57k1UoAcGBSuBBAAK
oUQDQgAEKNlv9Lyu406/hmj4r3ZfmtisJUvPThCasMGySrR4mST8LxLeO6NpsmKL
OVSNQgleZw6fu2ktLGFtObKTeu6z9w==
-----END EC PRIVATE KEY-----

显示私钥信息

// 显示私钥信息
$ openssl ec -in ecdsa_priv.pem -text -noout

输出

read EC key
Private-Key: (256 bit)
priv:
    05:34:7e:d2:08:6c:b7:42:44:e6:0e:65:c1:9c:73:
    ee:09:8c:0b:13:bd:82:35:a4:7f:44:8d:bc:79:ee:
    4d:54
pub:
    04:28:d9:6f:f4:bc:ae:e3:4e:bf:86:68:f8:af:76:
    5f:9a:d8:ac:25:4b:cf:4e:10:9a:b0:c1:b2:4a:b4:
    78:99:24:fc:2f:12:de:3b:a3:69:b2:62:8b:39:54:
    8d:42:09:5e:67:0e:9f:bb:69:2d:2c:61:6d:39:b2:
    93:7a:ee:b3:f7
ASN1 OID: secp256k1

从输出信息里面可以看到私钥信息和命名曲线的信息，密钥长度是 256 比特。

接下来获取公钥。

// 提取公钥
$ openssl ec -in ecdsa_priv.pem -pubout -out ecdsa_pub.pem

// 显示公钥
$ openssl ec -in ecdsa_pub.pem -pubin -text -noout

输出

// ecdsa_pub.pem
-----BEGIN PUBLIC KEY-----
MFYwEAYHKoZIzj0CAQYFK4EEAAoDQgAEKNlv9Lyu406/hmj4r3ZfmtisJUvPThCa
sMGySrR4mST8LxLeO6NpsmKLOVSNQgleZw6fu2ktLGFtObKTeu6z9w==
-----END PUBLIC KEY-----


read EC key
Public-Key: (256 bit)
pub:
    04:28:d9:6f:f4:bc:ae:e3:4e:bf:86:68:f8:af:76:
    5f:9a:d8:ac:25:4b:cf:4e:10:9a:b0:c1:b2:4a:b4:
    78:99:24:fc:2f:12:de:3b:a3:69:b2:62:8b:39:54:
    8d:42:09:5e:67:0e:9f:bb:69:2d:2c:61:6d:39:b2:
    93:7a:ee:b3:f7
ASN1 OID: secp256k1

生成签名

// 选择 sha256 作为 HASH 算法
$ openssl dgst -sha256 -sign ecdsa_priv.pem -out signature.txt plain.txt

输出

// signature.txt
0E^B JTH}Xi<88>)<8d>'È;þÆße<93>»Õ¦|?8^@<84>=gªA)F^K^B!^@°^U³<9d>F <83>ÐÄµb^^<81>ÿ<9b>b<92>Âæ½M0,"W$G,øÑRW

校验签名

// 校验签名
$ openssl dgst -sha256 -verify ecdsa_pub.pem -signature signature.txt plain.txt

输出

Verified OK

如果怀疑上面校验是否是真的，我们可以用另外一个文件来验证一下签名，比如换一个 txt

// 更换一个 txt 文件再次验证签名
$ openssl dgst -sha256 -verify ecdsa_pub.pem -signature signature.txt signature.txt

输出

Verification Failure

DSA 签名算法运算比 RSA 签名运算慢很多，但是 ECDSA 签名算法比 RSA 签名生成快的多，ECDSA 签名验证却比 RSA 签名验证相对慢一些。

从安全和速度综合考虑，在 DSA 和 ECDSA 中选一个，优先选择 ECDSA。

Reference：

《图解密码技术》

GitHub Repo：Halfrost-Field

Follow: halfrost · GitHub

Source: https://halfrost.com/digital_signature/

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

HTTPS-digital-signature.md

HTTPS-digital-signature.md

无处不在的数字签名

一、为什么需要数字签名？

二、什么是数字签名？

三、生成和验证数字签名

1. 直接对消息签名的方法

2. 对消息的散列值签名的方法

四、数字签名应用实例

1. 安全信息公告

2. 软件下载

3. 公钥证书

4. SSL/TLS

五、数字签名的实现方式

1. 用 RSA 生成签名

2. 用 RSA 验证签名

六、其他几种数字签名

1. ElGamal 方式

2. DSA

生成 DSA 密钥对

签名生成

签名验证

3. ECDSA

生成 ECDSA 密钥对

签名生成

验证签名

4. Rabin 方式

七、对数字签名的攻击

1. 中间人攻击公钥

2. 对单向散列函数的攻击

3. 利用数字签名攻击公钥密码

4. 潜在伪造

5. 其他攻击

八、数字签名无法解决的问题

九、OpenSSL 中的 RSA 数字签名

十、OpenSSL 中的 DSA 数字签名

十、OpenSSL 中的 ECDSA 数字签名

Files

HTTPS-digital-signature.md

Latest commit

History

HTTPS-digital-signature.md

File metadata and controls

无处不在的数字签名

一、为什么需要数字签名？

二、什么是数字签名？

三、生成和验证数字签名

1. 直接对消息签名的方法

2. 对消息的散列值签名的方法

四、数字签名应用实例

1. 安全信息公告

2. 软件下载

3. 公钥证书

4. SSL/TLS

五、数字签名的实现方式

1. 用 RSA 生成签名

2. 用 RSA 验证签名

六、其他几种数字签名

1. ElGamal 方式

2. DSA

生成 DSA 密钥对

签名生成

签名验证

3. ECDSA

生成 ECDSA 密钥对

签名生成

验证签名

4. Rabin 方式

七、对数字签名的攻击

1. 中间人攻击公钥

2. 对单向散列函数的攻击

3. 利用数字签名攻击公钥密码

4. 潜在伪造

5. 其他攻击

八、数字签名无法解决的问题

九、OpenSSL 中的 RSA 数字签名

十、OpenSSL 中的 DSA 数字签名

十、OpenSSL 中的 ECDSA 数字签名