我们此前已经学过线性回归和非线性回归,那为什么还需要神经网络了?
因为无论是线性回归还是逻辑回归都有这样一个缺点,即:当特征太多时,计算的负荷会非常大。举个例子:
当使用 x1 , x2 的多次项式进行预测时,回归算法可以很好地工作。之前已经看到过,使用非线性的多项式项,能够建立更好的分类模型。
但是,如果数据集有非常多的特征,例如大于100,当希望用这100个特征构建一个非线性的多项式模型,将是数量惊人的特征组合,即便我们只采用两两特征的组合 (x1x2+x1x3+x1x4+...+x2x3+x2x4+...+x99x100) ,也会有接近5000个组合而成的特征。特征的数量会以 O(n) 的复杂度来增加。这对于逻辑回归需要计算的特征太多了!
假设希望训练一个模型识别视觉对象(例如识别图片上是否是汽车)。一种方法是我们利用很多汽车的图片和很多非汽车的图片,然后利用这些图片上一个个像素的值(饱和度或亮度)来作为特征。
假如只选用灰度图片,每个像素则只有一个值(非RGB值),可以将每个图片的像素作为特征来训练逻辑回归算法,并利用像素值来判断图片上是否是汽车。
假如采用的是50*50像素的图片,则有2500个特征,如果进一步采用两两特征组合构成一个多项式模型,则有 25002/2 ≈ 3百万 个特征。复杂度太高了!逻辑回归已经不能很好处理,这时候就需要神经网络。
神经网络是一种很古老的算法,发明它最初的目的是制造模拟大脑的机器。
神经网络兴起于二十世纪八九十年代,应用得非常广泛。但在90年代的后期应用减少了。但最近,又东山再起。
- 其中一个原因是神经网络计算量偏大。由于近年计算机运行速度变快,能运行起大规模的神经网络。正由这个原因和其他技术因素,如今神经网络对许多应用来说是最先进的技术。
人类大脑可以学数学、微积分,而且能处理各种不同的事情。似乎如果你想要模仿大脑,你得写很多不同的软件来模拟所有这些五花八门的事情。不过能不能假设大脑做所有这些,不同事情的方法,不需要用上千个不同的程序。相反,大脑处理的方法,只需要一个单一的学习算法就可以了?尽管这只是一个假设,先来介绍一些这方面的证据:
- 神经系统科学家通过神经重接实验证实人体有同一块脑组织可以处理光、声或触觉信号,那么也许存在一种学习算法,可以同时处理视觉、听觉和触觉,而不是需要运行上千个不同的程序。也许需要做的就是找出一些近似的或实际的大脑学习算法,然后实现它大脑通过自学掌握如何处理这些不同类型的数据。
为了构建神经网络模型,我们先思考大脑中的神经网络是怎样的:每个神经元都被认为是一个处理单元,即神经核(Nucleus),它含有许多输入,即树突(Dendrite),并且有一个输出,即轴突(Axon)。神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络。如下图:
神经元利用微弱的电流进行沟通。这些弱电流也称作动作电位。所以如果神经元想要传递一个消息,它会通过它的轴突,发送一段微弱电流给其他神经元。
下图是一条连接到输入神经,或者连接另一个神经元树突的神经。右上角的神经元 A 通过轴突把消息传递给左下角的神经元 B,B有可能会把消息再传给其他神经元。
这就是所有人类思考的模型:神经元把收到的消息进行计算,并向其他神经元传递消息。这也是感觉和肌肉运转的原理。
如果你想活动一块肌肉,就会触发一个神经元给你的肌肉发送脉冲,并引起你的肌肉收缩。如果一些感官:比如说眼睛想要给大脑传递一个消息,那么它就像这样发送电脉冲给大脑的。
神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型。这些神经元(也叫激活单元,activation unit)采纳一些特征作为输出,并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为自身学习模型的神经元示例,在神经网络中,参数又可被称为权重(weight)。
其中 x1 , x2 , x3 是输入单元(input units),我们将原始数据输入给它们。 a1 , a2 , a3 是中间单元,它们负责将数据进行处理,然后呈递到下一层。最后是输出单元,它负责计算 hθ(x) 。 注意:这里 hθ(x)=1/(1+e-θTX)
神经元的神经网络,效果如下:
神经网络模型是许多逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。上图为一个3层的神经网络,第一层成为输入层(Input Layer),最后一层称为输出层(Output Layer),中间一层成为隐藏层(Hidden Layers)。我们为每一层都增加一个偏差单位(Bias unit),如下图所示。
神经网络模型的一些符号描述:
- ai(j) 代表第 j 层的第 i 个激活单元。
- Θ(j) 代表从第 j 层映射到第 j+1 层时的权重的矩阵,例如 θ(1) 代表从第一层映射到第二层的权重的矩阵。
- 其尺寸为:以第 j+1 层的激活单元数量为行数,以第 j 层的激活单元数加1为列数的矩阵。例如:上图所示的神经网络中 θ(1) 的尺寸为3*4(列加1是因为要对应 x0, a0 这样的bias,搞清楚权重矩阵的大小很重要!)。
那么对于上图中的神经网络,可得:
- a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
- a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
- a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
- hΘ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
上面进行的讨论只是将特征矩阵中的一行(一个训练实例)喂给了神经网络,我们需要将整个训练集都喂给我们的神经网络算法来学习模型。
每一个 a 都是由上一层所有的 x 和每一个 x 所对应的决定的。 我们把这样从左到右的算法称为前向传播算法(Forward Propagation)。
把 x , Θ , a 分别用矩阵表示:
我们可以得到 a = Θ · X 。
当然上式这非常取决于X本身是如何排列的,通常是X的每一行是一个样本,每一列是一个样本特征。
前向传播算法使用循环来计算,当然利用向量化的方法(Vectorized Computation)会使得计算更为简便。以上面的神经网络为例。
此外,为了简化公式,定义另外一个符号 z:
- z(j) = Θ(j-1) · a(j-1)
那么上面的例子可以描述如下:
我们令 z(2)=Θ(1)x ,则 a(2)=g(z(2)) ,计算后添加 a0(2)=1 。展开过程也就是:
我们令 z(3)=Θ(2)a(2) ,则 hΘ(x)=a(3)=g(z(3)) 。
上面的过程只讨论了对训练集中一个训练实例的计算。如果要对整个训练集计算,需要将训练集特征矩阵进行转置,使得同一个实例的特征都在同一列里。即
- z(2)=Θ(1)XT
- a(2)=g(z(2))
为了更好了了解神经网络的原理,我们把上面示例网络的左半部分遮住:
可以看到,右半部分其实就是一个逻辑回归模型:以 a0,a1,a2,a3 作为输入,并按照Logistic Regression的方式输出 hθ(x) 。
其实神经网络就像是逻辑回归,只不过我们把逻辑回归中的输入向量 [x1 ~ x3] 变成了中间层的 [a1(2) ~ a3(2)] ,即: hθ(x)=g(Θ0(2)a0(2)+Θ1(2)a1(2)+Θ2(2)a2(2)+Θ3(2)a3(2)) 我们可以把 a0, a1, a2, a3 看成更为高级的特征值,也就是 x0, x1, x2, x3 的进化体,并且它们是由 x 与 Θ 决定的,因为是梯度下降的,所以 a 是变化的,并且变得越来越厉害,所以这些更高级的特征值远比仅仅将 x 次方厉害,也能更好的预测新数据。这就是神经网络相比于逻辑回归和线性回归的优势。
神经网络架构是不同层(Layer)之间的链接方式。包括:
- 有多少层
- 每一层有多少激活单元
第一层是输入层(Input Layer),最后一层是输出层(Output Layer),中间的是影藏层(Hidden Layer)。
神经网络能够通过学习得出其自身的一系列特征。在普通的逻辑回归中,我们被限制为使用数据中的原始特征 x1,x2,...,xn ,我们虽然可以使用一些二项式项来组合这些特征,但是我们仍然受到这些原始特征的限制。在神经网络中,原始特征只是输入层,在我们上面三层的神经网络例子中,第三层也就是输出层做出的预测利用的是第二层的特征,而非输入层中的原始特征,我们可以认为第二层中的特征是神经网络通过学习后自己得出的一系列用于预测输出变量的新特征。
神经网络中,单层神经元(无中间层)的计算可用来表示逻辑运算,比如逻辑与(AND)、逻辑或(OR)。
逻辑与(AND)
下图中左半部分是神经网络的设计与输出层表达式,右边上部分是Sigmod函数,下半部分是真值表。
我们可以用这样的一个神经网络表示AND 函数:
其中 θ0=-30,θ1=20,θ2=20 我们的输出函数 hθ(x) 即为: hΘ(x)=g(-30+20x1+20x2)
所以我们有: hΘ(x) ≈ x1 AND x2
逻辑或(OR)
OR与AND整体一样,区别只在于 Θ 的取值不同。
--- 二元逻辑运算符(BINARY LOGICAL OPERATORS)当输入特征为布尔值(0或1)时,我们可以用一个单一的激活层可以作为二元逻辑运算符,为了表示不同的运算符,我们只需要选择不同的权重即可。下图的神经元(三个权重分别为-30,20,20)可以被视为作用同于逻辑与(AND):
下图的神经元(三个权重分别为-10,20,20)可以被视为作用等同于逻辑或(OR): 下图的神经元(两个权重分别为 10,-20)可以被视为作用等同于逻辑非(NOT):可以利用神经元来组合更为复杂的神经网络以实现复杂的运算。例如要实现XNOR功能(输入的两个值必须一样,均为1或均为0),即 XNOR=(x1,AND,x2) OR((NOT,x1) AND(NOT,x2))
- 首先构造一个能表达 (NOT,x1)AND(NOT,x2) 部分的神经元:
- 然后将表示AND的神经元和表示 (NOT,x1)AND(NOT,x2) 的神经元以及表示OR的神经元进行组合:
这样就得到了一个 XNOR 运算符功能的神经网络。按这种思路你可以逐渐构造出越来越复杂的函数和特征值。这就是神经网络的厉害之处。
一个神经网络做手写数字识别的演示视频
(上面的视频是Youtube的,如果无法翻墙的,可访问爱奇艺上的链接)
当分类问题不止两种分类时( y=1,2,3…. ),比如如果我们要训练一个神经网络算法来识别路人、汽车、摩托车和卡车。
- 在输出层我们应该有4个值。例如,第一个值为1或0用于预测是否是行人,第二个值用于判断是否为汽车。
- 输入向量 x 有三个维度,两个中间层,输出层4个神经元分别用来表示4类,也就是每一个数据在输出层都会出现 [a b c d]T ,且 a,b,c,d 中仅有一个为1,表示当前类。
下面是该神经网络的可能结构示例:
神经网络算法的输出结果为四种可能情形之一:
首先介绍一些符号计法:
- 假设神经网络的训练样本有 m 个
- 每个包含一组输入 x 和一组输出信号 y
- L 表示神经网络层数
- SI 表示每层的神经元个数( Sl 表示输出层神经元个数), SL 代表最后一层中处理单元的个数
将神经网络的分类定义为两种情况:二类分类和多类分类,
- 二类分类: SL=0, y=0, or, 1 表示哪一类;
- K 类分类: SL=k, yi=1 表示分到第 i 类; (k>2)
也可以参考下图:
我们回顾逻辑回归问题中我们的代价函数为:
在逻辑回归中,我们只有一个输出变量,又称标量(scalar),也只有一个因变量 y ,但是在神经网络中,我们可以有很多输出变量,我们的 hθ(x) 是一个维度为 K 的向量,并且我们训练集中的因变量也是同样维度的一个向量,因此我们的代价函数会比逻辑回归更加复杂一些,为:
但神经网络代价函数的思想还是和逻辑回归代价函数是一样的,希望通过代价函数来观察算法预测的结果与真实情况的误差有多大,唯一不同的是,对于每一行特征,我们都会给出 K 个预测,基本上我们可以利用循环,对每一行特征都预测 K 个不同结果,然后在利用循环在 K 个预测中选择可能性最高的一个,将其与 y 中的实际数据进行比较。
注意:正则化的那一项排除了每一层 Θ0 的和。最里层的循环 j 循环所有的行(由 sl+1 层的激活单元数决定),循环 i 则循环所有的列,由该层( sl 层)的激活单元数所决定。即: hΘ(x) 与真实值之间的距离为每个样本-每个类输出的加和,对参数进行正则化(Regularization)的Bias项处理所有参数的平方和。 (注意,Θ 是 以第 sl+1 层的激活单元数量为行数,以第 sl+1 为列数的矩阵,公式里 i = 1开始,相当于把 Θ[:,0] 忽略了,而 Θ 的行数 j 本身就是从1开始的。)
之前我们在计算神经网络预测结果的时候我们采用了一种正向传播方法,我们从第一层开始正向一层一层进行计算,直到最后一层的 hθ(x) 。现在,为了计算代价函数的偏导数
,我们需要采用一种反向传播算法,也就是首先计算最后一层的误差,然后再一层一层反向求出各层的误差,直到倒数第二层。以一个例子来说明反向传播算法。假设我们的训练集只有一个样本 (x(1),y(1)) ,我们的神经网络是一个四层的神经网络,其中 K=4,SL=4,L=4 :
前向传播算法:
激活函数 g 一般是非线性可微函数。常用作激活函数的是逻辑函数:
其导数的形式为:
首先,我们定义 δj(l) 为第 (l) 层第 j 个神经元对最终结果导致的误差(Error),误差是相对于每个神经元的输入 z 来讲的。 定义:
由根据链式法则可得:
可得:
对于上面这个简单的神经网络,每一层的 δ(l) 计算如下:
- 从最后一层的误差开始计算,误差是激活单元的预测( a(4) )与实际值( yk )之间的误差( k=1:k )。则
- 利用这个误差值来计算前一层的误差: δ(3)=(Θ(3))Tδ(4) * g'(z(3)),其中:
- g'(z(3)) 是 S 形函数的导数, g'(z(3))=a(3) * (1-a(3)) 。
- (θ(3))Tδ(4) 则是权重导致的误差的和。
-
下一步是继续计算第二层的误差: δ(2)=(Θ(2))Tδ(3) * g'(z(2))
-
第一层是输入变量,不存在误差。
我们有了所有的误差的表达式后,便可以计算代价函数的偏导数了,假设 λ=0 ,即我们不做任何正则化处理时有:
注意,上面的公式是由 δ 的定义决定的。
再次说明上式的一些符号:
- l 代表目前所计算的是第几层。
- j 代表目前计算层中的激活单元的下标,也将是下一层的第 j 个输入变量的下标。
- i 代表下一层中误差单元的下标,是受到权重矩阵中第 i 行影响的下一层中的误差单元的下标。
当然上面没考虑正则化,如果考虑正则化处理,并且训练集是一个矩阵而非向量。在上面的特殊情况中,需要计算每一层的误差单元来计算代价函数的偏导数。更为一般的情况,需要为整个训练集计算误差单元,此时的误差单元也是一个矩阵,我们用 Δ(l)ij 来表示这个误差矩阵。第 l 层的第 i 个激活单元受到第 j 个参数影响而导致的误差。
那么上面的算法可以描述为:
即首先用正向传播方法计算出每一层的激活单元,利用训练集的结果与神经网络预测的结果求出最后一层的误差,然后利用该误差运用反向传播法计算出直至第二层的所有误差。
在求出了 Δij(l) 之后,我们便可以计算代价函数的偏导数了,计算方法如下:
- Dij(l):=(1/m)Δij(l) + λΘij(l), if j != 0
- Dij(l):=(1/m)Δij(l), if j=0
上面的_Dij(l)_就是可以最终用来在梯度下降中更新权重Θ的。
前向传播算法:
反向传播算法做的是:
对一个复杂的模型(例如神经网络)使用梯度下降算法时,可能会存在不容易察觉的错误。就是说,虽然代价函数(Cost function)看上去在不断减小,但最终的结果可能并不是最优解。
为了避免这样的问题,我们采取一种叫做梯度的数值检验(Numerical Gradient Checking)方法。这种方法的思想是通过估计梯度值来检验我们计算的导数值是否符合预期。
对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点,然后计算两个点的平均值用以估计梯度。即对于某个特定的 θ ,我们计算出在 θ - ϵ 处和 θ + ϵ 的代价值( ϵ 是一个非常小的值,通常选取0.001),然后求两个代价的平均,用以估计在 θ 处的代价值。
gradApprox = (J(theta + eps) – J(theta - eps)) / (2*eps)当 θ 是一个向量时,我们则需要对偏导数进行检验。因为代价函数的偏导数检验只针对一个参数的改变进行检验,下面是一个只针对 θ1 进行检验的示例: ((∂)/(∂θ1))=((J(θ1+ϵ1,θ2,θ3...θn)-J(θ1-ϵ1,θ2,θ3...θn))/(2ϵ))
最后我们还需要对通过反向传播方法计算出的偏导数进行检验。
根据反向传播算法,计算出的偏导数存储在矩阵 Dij(l) 中。检验时,我们要将该矩阵展开成为向量,同时我们也将 θ 矩阵展开为向量,我们针对每一个 θ 都计算一个近似的梯度值,将这些值存储于一个近似梯度矩阵 gradApprox 中,最终将得出的这个矩阵同 Dij(l) 进行比较。预期的情况是: gradApprox ≈ D
注意:请在开始训练你的模型之前,把梯度检验禁用掉,因为它非常耗时!
任何优化算法都需要一些初始的参数。到目前为止我们都是初始所有参数为0,这样的初始方法对于逻辑回归来说是可行的,但是对于神经网络来说是不可行的。如果我们令所有的初始参数都为0,这将意味着我们第二层的所有激活单元都会有相同的值。同理,如果我们初始所有的参数都为一个非0的数,结果也是一样的。
我们通常初始参数为正负ε之间的随机值,假设我们要随机初始一个尺寸为10×11的参数矩阵,代码如下:
import numpy as np
eps = np.power(10, -5)
Theta1 = np.random.rand(10, 11) * (2*eps) – eps小结使用神经网络时的步骤:
第一件要做的事是选择网络结构,即决定选择多少层以及决定每层分别有多少个单元。
- 第一层的单元数即我们训练集的特征数量。
- 最后一层的单元数是我们训练集的结果的类的数量。
- 如果隐藏层数大于1,(默认情况下)每个隐藏层的单元个数相同,通常情况下隐藏层单元的个数越多越好。
- 我们真正要决定的是隐藏层的层数和每个中间层的单元数。
- 参数的随机初始化
- 利用正向传播方法计算所有的 hθ(x)
- 编写计算代价函数 J 的代码
- 利用反向传播方法计算所有偏导数
- 利用数值检验方法(Gradient Checking)检验这些偏导数
- 使用优化算法来最小化代价函数
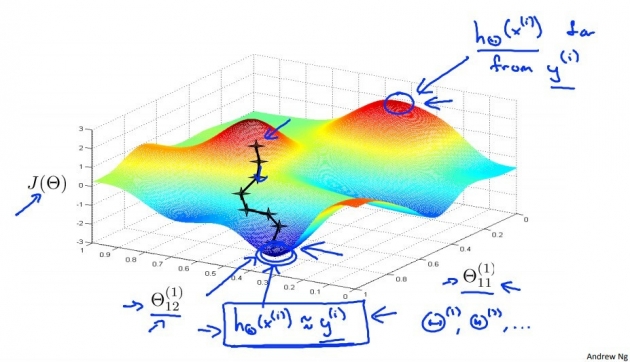
最后,请记住这张图,它很好的体现了神经网络和梯度下降的原理:
一个1992年用神经网络做自动驾驶的的演示视频
(上面的视频是Youtube的,如果无法翻墙的暂无墙内地址..)
在图中你依稀能看出一条道路,朝左延伸了一点,又向右了一点,然后上面的这幅图,你可以看到一条水平的菜单栏显示的是驾驶操作人选择的方向。就是这里的这条白亮的区段显示的就是人类驾驶者选择的方向。比如:最左边的区段,对应的操作就是向左急转,而最右端则对应向右急转的操作。因此,稍微靠左的区段,也就是中心稍微向左一点的位置,则表示在这一点上人类驾驶者的操作是慢慢的向左拐。这幅图的第二部分对应的就是学习算法选出的行驶方向。并且,类似的,这一条白亮的区段显示的就是神经网络在这里选择的行驶方向,是稍微的左转,并且实际上在神经网络开始学习之前,你会看到网络的输出是一条灰色的区段,就像这样的一条灰色区段覆盖着整个区域这些均称的灰色区域,显示出神经网络已经随机初始化了,并且初始化时,我们并不知道汽车如何行驶,或者说我们并不知道所选行驶方向。只有在学习算法运行了足够长的时间之后,才会有这条白色的区段出现在整条灰色区域之中。显示出一个具体的行驶方向这就表示神经网络算法,在这时候已经选出了一个明确的行驶方向,不像刚开始的时候,输出一段模糊的浅灰色区域,而是输出一条白亮的区段,表示已经选出了明确的行驶方向。
ALVINN (Autonomous Land Vehicle In a Neural Network)是一个基于神经网络的智能系统,通过观察人类的驾驶来学习驾驶,ALVINN能够控制NavLab,装在一辆改装版军用悍马,这辆悍马装载了传感器、计算机和驱动器用来进行自动驾驶的导航试验。实现ALVINN功能的第一步,是对它进行训练,也就是训练一个人驾驶汽车。然后让ALVINN观看,ALVINN每两秒将前方的路况图生成一张数字化图片,并且记录驾驶者的驾驶方向,得到的训练集图片被压缩为30x32像素,并且作为输入提供给ALVINN的三层神经网络,通过使用反向传播学习算法,ALVINN会训练得到一个与人类驾驶员操纵方向基本相近的结果。一开始,我们的网络选择出的方向是随机的,大约经过两分钟的训练后,我们的神经网络便能够准确地模拟人类驾驶者的驾驶方向,对其他道路类型,也重复进行这个训练过程,当网络被训练完成后,操作者就可按下运行按钮,车辆便开始行驶了。
每秒钟ALVINN生成12次数字化图片,并且将图像传送给神经网络进行训练,多个神经网络同时工作,每一个网络都生成一个行驶方向,以及一个预测自信度的参数,预测自信度最高的那个神经网络得到的行驶方向。比如这里,在这条单行道上训练出的网络将被最终用于控制车辆方向,车辆前方突然出现了一个交叉十字路口,当车辆到达这个十字路口时,我们单行道网络对应的自信度骤减,当它穿过这个十字路口时,前方的双车道将进入其视线,双车道网络的自信度便开始上升,当它的自信度上升时,双车道的网络,将被选择来控制行驶方向,车辆将被安全地引导进入双车道路。
这就是基于神经网络的自动驾驶技术。当然,我们还有很多更加先进的试验来实现自动驾驶技术。在美国,欧洲等一些国家和地区,他们提供了一些比这个方法更加稳定的驾驶控制技术。但我认为,使用这样一个简单的基于反向传播的神经网络,训练出如此强大的自动驾驶汽车,的确是一次令人惊讶的成就。
- 推荐访问Google Drive的共享,直接在Google Colab在线运行ipynb文件:
- 不能翻墙的朋友,可以访问GitHub下载: