-
Notifications
You must be signed in to change notification settings - Fork 44
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
fix 369 #370
base: main
Are you sure you want to change the base?
fix 369 #370
Conversation
|
Check out this pull request on See visual diffs & provide feedback on Jupyter Notebooks. Powered by ReviewNB |
for more information, see https://pre-commit.ci
|
Thanks @briochemc. This is helpful but also potentially breaking peoples code. I am planning to do another deep dive on the vertex order (to solve e.g. #368 ) and will try to ship this with any other updates as a major update! |
|
That is a smart way to test the consistency. I think this is implicitly ensured in my hacky solution in #368 (comment), but I will definitely try to use that part of the logic over there. |
|
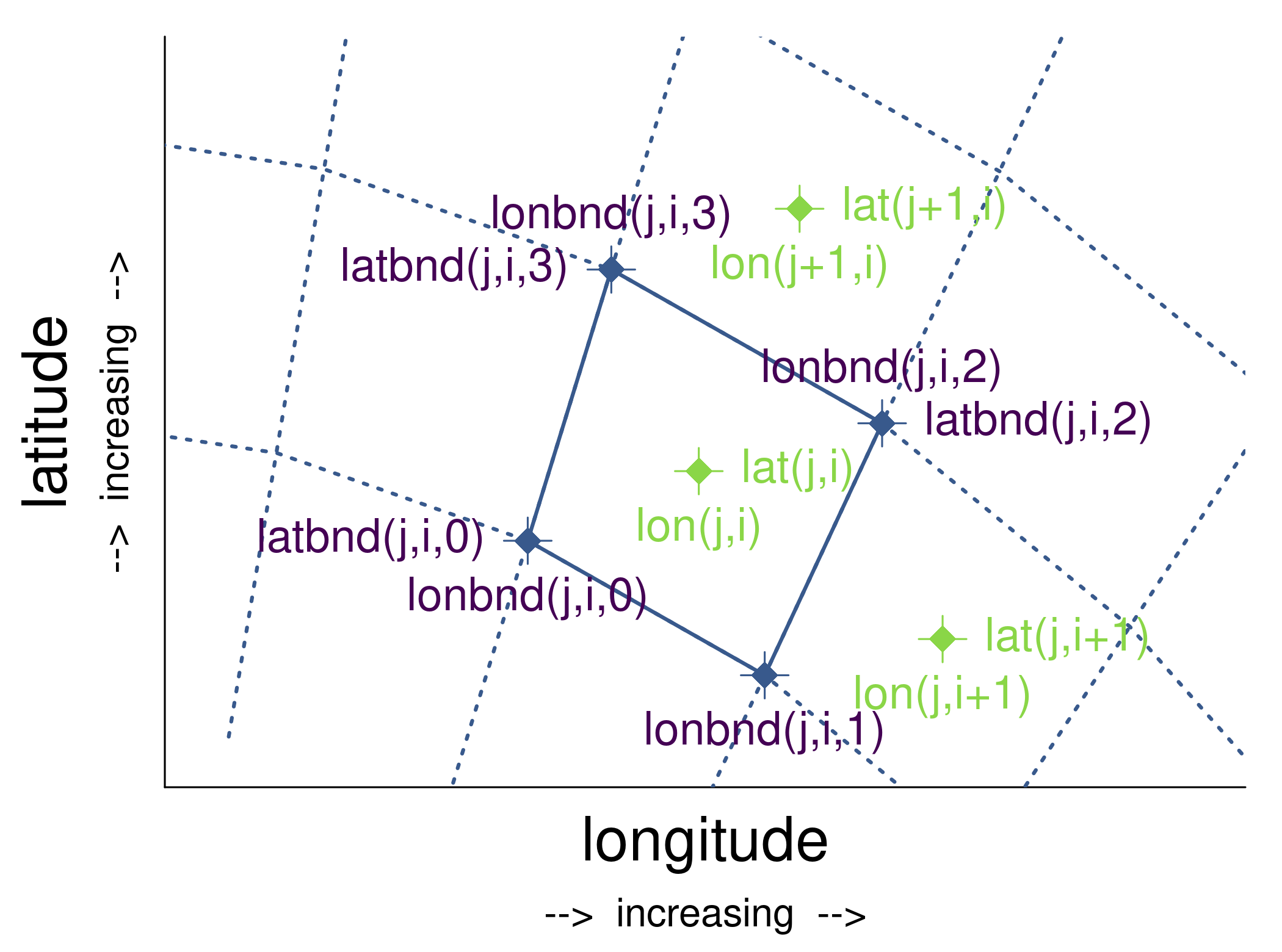
In case this helps your implementation in xmip, I have implemented my own in Julia in OceanTransportMatrixBuilder.jl in a slightly different way, which I think is clearer. I just intersect the set of vertices of cells (i,j), (i+1,j), and (i,j+1) to determine the vertex index order. Code is located here and looks like this (with 1-indexing in Julia): # The default orientation is the following:
#
# 4 ────┐ 3
# │
# 1 ────┘ 2
#
# Given lon_vertices and lat_vertices, find the permutation
# that sorts the vertices in that order.
function vertexpermutation(lon_vertices, lat_vertices)
# Make sure the vertices are in the right shape (4, nx, ny)
@assert size(lon_vertices, 1) == size(lat_vertices, 1) == 4
# Take the first grid cell
i = j = 1
# Turn the vertices into points
points = collect(zip(lon_vertices[:, i, j], lat_vertices[:, i, j]))
points_east = collect(zip(lon_vertices[:, i+1, j], lat_vertices[:, i+1, j]))
points_north = collect(zip(lon_vertices[:, i, j+1], lat_vertices[:, i, j+1]))
# Find the common points
common_east = intersect(Set(points), Set(points_east))
common_noth = intersect(Set(points), Set(points_north))
# Find the indices of the common points
idx_east = findall(in(common_east), points)
idx_north = findall(in(common_noth), points)
idx3 = only(intersect(idx_east, idx_north)) # common to all 3 cells
idx2 = only(setdiff(idx_east, idx3)) # common to (i,j) and (i+1,j) only
idx4 = only(setdiff(idx_north, idx3)) # common to (i,j) and (i,j+1) only
idx1 = only(setdiff(1:4, idx2, idx3, idx4)) # only in (i,j)
return [idx1, idx2, idx3, idx4]
endVisual check part of my local tests for my sanity that may be a helpful illustration: |

pre-commit run --all-fileswhats-new.rstapi.rst