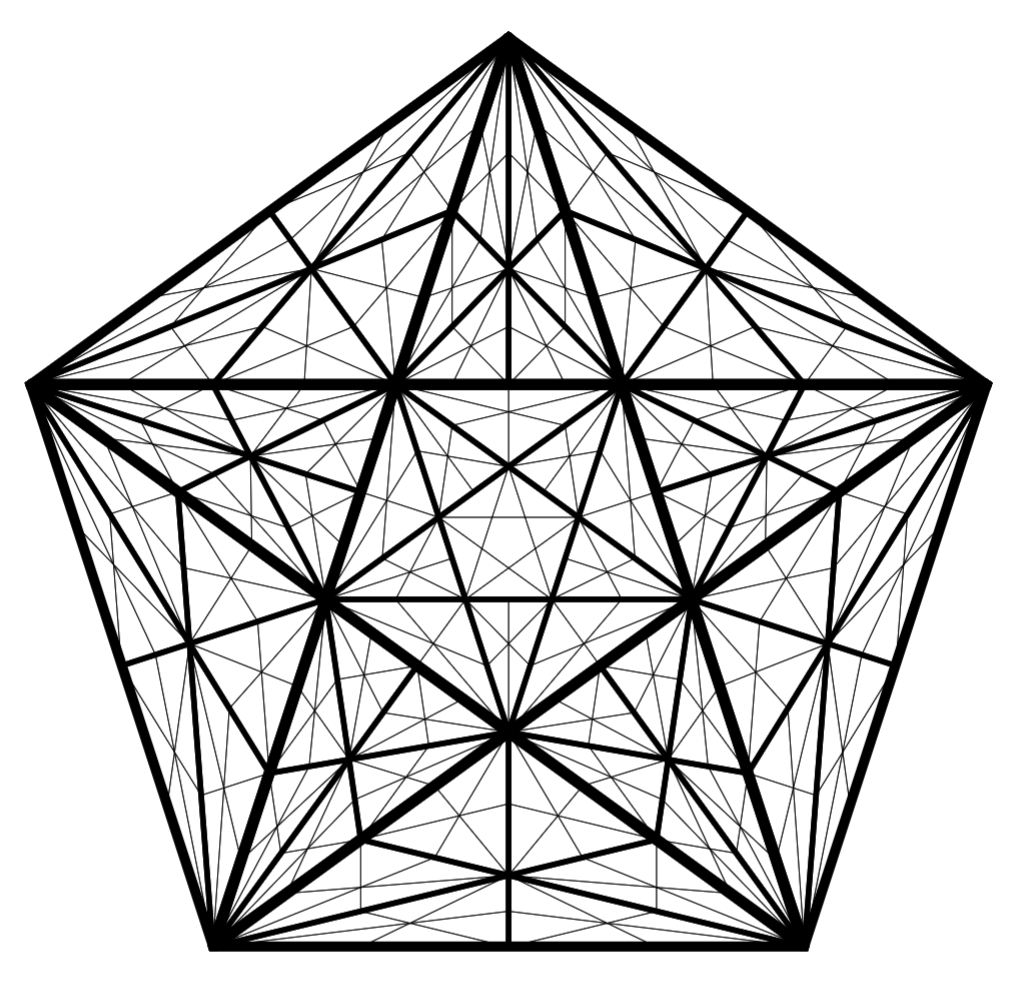
The design consists of pentagons (hence "pentafractal") and triangles. It's based on nested pentagrams- that is, a succession of five-pointed stars, each inscribed in the central pentagon of the previous one. I wanted the design to have more-uniformly-sized pieces, so whenever I draw a new central pentagram, I also fragment all the triangles outside the central pentagon. Each triangle is fragmented into six pieces by splitting along its medians. Using medians instead of angle bisectors makes splits from adjacent triangles align, since every split occurs through the midpoint of a triangle's side.
To draw these designs, I used Java in combination with the Tikz drawing package of LaTeX. The code in Pentaglass.java performs geometric calculations and prints Tikz code for the resulting shape. The output can be copy-pasted into a tikzpicture environment to display the fractal. The recursive depth, size, and location of the fractal are specified as parameters to the Java pentafractal method, and any Tikz format options, such as line width and fill color, may be passed to the toLatex method as a string. Since the geometry and LaTeX are handled separately, the program could easily be adapted for other graphics platforms.
The design looks particularly stunning if each shape is given a random-color fill. Random coloring is accomplished with a \randomcolor command defined in the preamble of the LaTeX document, which redefines randomcolor as a new RGB color each time it is invoked.
For more examples of the effects that can be made with this design, take a look at Pentaglas_fractal.tex and its compilation, Pentaglass_fractal.pdf. I encourage you to generate your own! Expect it to take under a minute to generate code for a fractal with 4 levels of recursion, and 15 seconds or less to compile the corresponding LaTeX document; the time increases about tenfold for each level of recursion.